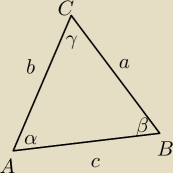matematykaszkolna.pl
Tw sinusów dowód mr9: rysunekw trójkącie abc dane są c=3 sinγ=0,25 oraz a2−b2=4. udowodnij że sin(α−β)=1/9
1 kwi 23:23
Eta: Z tw. sinusów
c a b 
=12=
=
⇒ b=12sinβ , a=12sinα
sinγ sinα sinβ 
i α+β=180o−γ ⇒ sin(α+β)= −sinγ=−1/4
 1 
a2−b2=(a−b)(a+b)⇒(sinα−sinβ)(sinα+sinβ)=
⇒ sin(α+β)*sin(α−β)=1/36
 36 
 1 1 1 
to −
*sin(α−β)=
⇒ sin(α−β) = −
 4 36 9 
2 kwi 01:05
an: dlaczego − a > b ⇒ α > β
2 kwi 10:44
Eta: Poprawiam Wkradł mi się błędny zapis (sorry
 1 
sin(α+β)= sn(180o−γ)= +sinγ= +
 4 
............................. ...........................
 1 1 1 
to +
*sin(α−β)=
⇒ sin(α−β)= +
 4 36 9 
2 kwi 12:58
mr9: Wytłumaczysz dlaczego (sinα−sinβ)(sinα+sinβ)=1/36 ⇒ sin(α+β)*sin(α−β)=1/36 ?
2 kwi 17:40
Adamm:
 α+β α−β 
sinα+sinβ=2sin(
)cos(
)
 2 2 
 α−β α+β 
sinα−sinβ=2sin(
)cos(
)
 2 2 
 α+β α−β α−β α+β 
2sin(
)cos(
)*2sin(
)cos(
)=
 2 2 2 2 
=sin(α+β)sin(α−β)
2 kwi 17:42