dowody, geometria aldona: witam bardzo prosze o pomoc w zadankach, probowałam je juz na wiele sposobow ale ni jak akurat te mi nie wychodzą. 1.w trójkącie o bokach długosci a,b,c poprowadzono odcinki długosci x,y,z styczne do okręgu wpisanego w ten trójkąt, mające końce na bokach trójkąta i równoległe odpowiednio do boków długości a,b,c. Wykaż że: x/a y/b +z/c = 1 2.w trójkacie prostokatnym ABC z wierzchołka kąta prostego C poprowadzono wysokość CD i w kazdy z trojkątow ABC, ACD, BCD wpisano okrąg. Wykaz , ze suma promieni tych okręgów równa się wysokości CD.

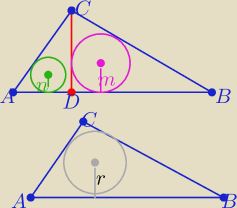
Eta: 2/ oznaczam długości promieni tych okręgów: n , m i r 2r=AC+BC−AB 2n=AD+DC−AC 2m=DB+DC−BC +−−−−−−−−−−−−−−−−−−−−−−−− 2r+2n+2m= AD−AB+DB+2CD i AB=AD+DB to 2r+2n+2m=AD−AD−DB+DB+2CD r+n+m=CD=h

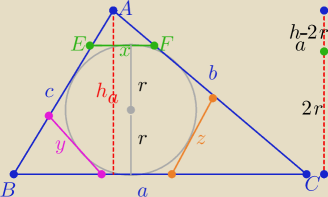
Eta: Z podobieństwa trójkątów AEF i ABC z cechy (kkk)

x		ha−2r		r
	=		=1−2
a		ha		ha

	y		r		z		r
oraz ..		=1−2		i		=1−2
	b		hb		c		hc

2P=a*h_a =b*h_b=c*h_c =r*(a+b+c) dodając stronami otrzymujemy

x

y

z

ar

br

cr

r(a+b+c)

+

+

=3−(

+

+

)= 3−

= 3−2=1

a

b

c

P

P

P

P

zatem:

	x		y		z
		+		+		=1
	a		b		c

c.n.w

aldona: dziękuje bardzo!