Zadanie okrąg i dwie proste, błąd w moim rozumowaniu? S: Rozwiązywałem następujące zadanie: Proste o równaniach y = x + 3, y = 2x + 5 zawierają średnice okręgu o, do którego należy punkt P = (3,2). Znajdź równanie okręgu o. Zadanie łatwo zrobić tak, że przyrówna się proste do siebie i znajdzie punkt przecięcia, czyli środek okręgu, ALE... Chciałem zobaczyć co jak zrobi się to trochę naokoło i zrobiłem coś takiego: f(a) = a + 3 g(a) = 2a + 5 Jeden z punktów na obu prostych to środek, więc równanie okręgu można zapisać: (x−a)² + (y −a − 3)² = r² lub (x−a)² + (y −2a − 5)² = r² Ale wiemy, że do okręgu należy punkt P, więc równania można zapisać: (3 − a)² + (2 − a − 3)² = r² lub (3 − a)² + (2 − 2a − 5)² = r² Tutaj przyrównałem do siebie, oba równania, myślałem, że dostane równanie kwadratowe z deltą równą zero, która wskaże środek okręgu, ale dostałem delte dodatnią i dwa rozwiązania. Jednym z nich było a = −2, które to jest wynikiem, który dostaniemy po przyrównaniu do siebie prostych, a drugim a = − 4/3 Pytanie brzmi, czy gdzieś się pomyliłem w rozumowaniu lub obliczaniach? Dlaczego dostałem dwa wyniki? Przecież dwie proste przecinają się w tylko jednym punkcie.

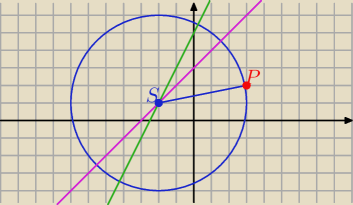
Eta: Rozwiązując układ równań otrzymasz współrzędne środka S y=x+3 y=2x+5 S(−2,1) to r²=|SP|²= ..... =26 o: (x+2)²+(y−1)²=26 i po ptokach

Powracający: Ale jak nie bedzie ptakow to kukułka w maju nie okuka z pieniedzy. Dzieciol nie bedzie stukal po debie . Jaskolki nie beda lataly nisko i bedzie wiadomo ze bedzie padal deszcz

S: Eta, przeczytaj pytanie jeszcze raz. Ja wiem o tym sposobie, wspominałem o nim. Moje pytanie jest inne: Dlaczego mój sposób nie działa, a raczej działa w połowie. Na chłopski rozum powinienem dostać delte 0, a mam dwa środki okręgu...

===: ... a co z ORŁEM Z WISŁY

Powracający: Juz nie poleci

S: Wiecie, ptaki ptakami, ale ktoś podpowie co jest na rzeczy z zadaniem?

Eta: @ S ... sorry ale nie chciało mi się czytać Twojego "wypracowania"

S: Wybaczam, wybaczam, ale co jest źle? Dlaczego ten punkt w ogóle wychodzi?

===: −4≠4 ale podniosę obustronnie do kwadratu 16=16

S: No wiem i wiem, że ten drugi punkt spełnia tylko równanie dla kwadratów, ALE na jakiej podstawie powinienem go wywalić na sam koniec? W sensie jak rozpoznać, że akurat ten trzeba wywalić.

Jack: musialbys na sam koniec sprawdzic... u Ciebie tamte dwie proste dla a=−4/3 sie nie przetna.

Jack: skoro sie tam nie przecinaja to nie ma tam srodka...

S: No oczywiscie. Ale skoro robie układ równań, to teorytycznie z zależnosci powinny mi wyjść rozwiązania spełniające wszystkie równania wewnątrz układu − a nie wychodzą. Dlaczego?

===: bo jedno spieprzone działanie i już "se ne wrati"

3Silnia&6: Bo to porownywanie dwoch rownan okregow dla jednakowych promieni nie "ödpowiada"na pytanie, w ktorym punkcie proste f i g sie przetna (czyli dla jakich x, wartosc y jest taka sama) tylko dla jakich x² wartosc y² jest taka sama Uzalezniajac y od x, wyznaczyles rozwiazanie dla jkakich x wartosc |y| jest taka sama, gdybys podstawil do rownania okregu x(y) ( w toich oznaczeniach przyjme, ze f(a) = b ) czyli takie rownaianie f(a) = a + 3 = b ⇒ a = b − 3 g(a) = 2a + 5 = b ⇒ a = b2 + 5/2 (3 − (b − 3) )2 + (2 − b)2 = r² lub (3 − (b2 + 5/2))^^2 + (2 − ^b)² = r² otrzymasz y dla ktorego warotsci |x| sa takie same