trapez, trudne paula: zad1 W trapezie ABCD gdzie AB∥CD i AB>CD Na podstawie CD obrano punkt P tak,że ||CP|/|PD|=16/9 Przedłużenie ramienia BC przecina się z prostą AP w punkcie E Przekątna BD przecina prostą AE w punkcie M Wykaż,że |AM| : |MP|=4:1 zad2 Na zewnątrz przeciwprostokątnej AB trójkąta prostokątnego ABC w którym suma długości przyprostokątnych jest równa k zbudowano kwadrat Wykaż ,że odległość środka kwadratu od wierzchołka kąta prostego

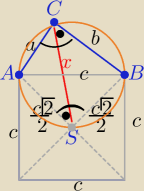
	√2(a+b)
wynosi
	2

Nie mogę sobie poradzić z tymi zadaniami Proszę o pomoc

===:

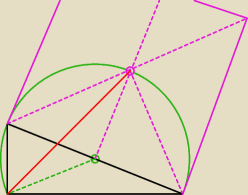
Eta: 2/ na czworokącie ASBC można opisać okrąg ( dlaczego? .. odpowiedz sama to można skorzystać z twierdzenia Ptolemeusza ( poczytaj o tym twierdzeniu u "cioci Wiki"

	c√2		c√2
i mamy a*		+b*		= c*x /: c≠0
	2		2

	√2
		(a+b)=x −−− teza
	2

	√2
lub a+b=k to x=		*k
	2

c.n.w

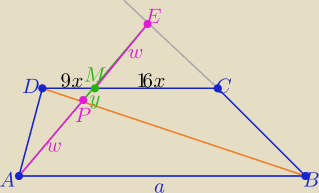Eta: Fajne zadanko Z treści zadania wprowadzam odpowiednie oznaczenia na rys. Dwa razy z podobieństwa trójkątów z cechy (kkk) ΔABP∼ΔDPM i ΔABE ∼ΔCME

	a		w		a		2w+y		y
		=		i		=		=2+
	9x		y		16x		w		w

	w
oznaczam		=t, t>0
	y

	9xt		1
to: a=9xt , x>0 i		=2+		/*16t
	16x		t

zatem 9t²−32t−16=0 , Δ= 1600 , √Δ=40

	32+40		w
t=		=4=
	18		y

	w		|AP|
to		=		=4 : 1
	y		|MP|

c.n.w