Rackunek różniczkowy i parametr k. jsn: Wyznacz te wartości parametru k dla których równanie x³−9x=k w przedziale <0;3> ma dwa rozwiązania. Kiełbasa, odp: (−6√3; 0> Kompletnie nie rozumiem zadań z parametrem "po prawej stronie", więc proszę o w miarę szczegółuwe wytłumaczenie.

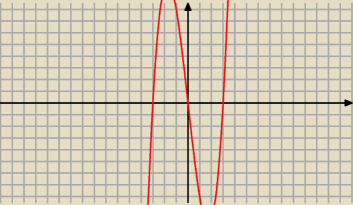
Adamm: f(x)=x³−9x f'(x)=3x²−9 mamy dwa ekstrema, √3 oraz −√3 rysujesz, teraz chyba już widać?

jsn: Widać, dzięki

Janek191: x*( x² − 9) = x*(x − 3)*(x + 3) = k Niech f(x) = x³ − 9 x f '(x) = 3 x² 9 = 0 ⇔ x = −√3 lub x = √3 x = √3 ∊ < 0, 3> Dla x = √3 funkcja f ma minimum lokalne y = f(√3) = 3√3 − 9√3 = − 6√3 Zatem dla k ∊ ( − 6√3, 0 > równanie ma dwa pierwiastki w < 0, 3 >. k₁ = − 5√3 k₂ = 0 k₃ = − 6√3

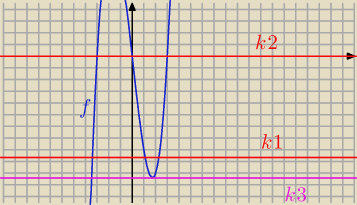
dobry_czlowiek: ale k1 i k2 nie moga byc bo na wykresie widac ze przykmują 3 wartości(w 3 punktach przecina wykres)

chichi: Ale czyś Ty czytał polecenie? NA PRZEDZIALE [0,3]