matura styczen2006-zad11 zad nie dajace mi spokoju: Zadanie pochodzi z matury ze stycznia 2006roku Zadanie 11. Wyznacz dziedzine i naszkicuj wykres funkcji f danej wzorem F(m)=x₁*x₂,gdzie x₁,x₂ sa roznymi pierwiastkami rownania (m+2)x²−(m+2)²x+3m+2=0, w ktorym mnalezy do R\{−2} wyliczylam juz dziedzine tego rownania Mnalezy (−niesko;−6)suma((−2;0)suma(0;+niesko) i nie wiem co dalej nie pamietam jak trzeba utworzyc wzor tej funkcji. Moglby ktos pomoc? rozwiazac dalej i pokazac krok po kroku? ps nie zalezy mi na tym zeby zrobic zadanie ale zrozumiec to czego nie wiem

zad nie dajace mi spokoju: nikt nie pomoze?:(

Ezop: podpowiem aby istniały dwa różne pierwiastki tego równania to: m+2≠0 i Δ >0

	c
wówczas: x1*x2=		−−− to druga część wzoru Viete'a
	a

	3m+2
f(m) =		, to Df: m€R\{−2}
	m+2

f(m) jest funkcją homograficzną ( wykresem jest hiperbola) ale tylko w przedziale dla m spełniajacego warunek na deltę( wyznacz ten przedział)

	3m+6 −4		3(m+2)−4		4
f(m) =		=		= 3 −
	m+2		m+2		m+2

dasz już teraz radę darysować ten wykres ( uwzględnij warunek Δ>0

Ezop: jest ok (moje niedopatrzenie , że miałaś już wyznaczoną tę dzidzinę ostatecznie D_f= ( −∞, −6)U(−2,0)U(0,∞)

zad nie dajace mi spokoju: no nie to tak prosto faky wystarczy z vieta dziekuje

Ezop:

zad nie dajace mi spokoju: a dlaczego tak przeksztalcilas ten wykres? dodalas 6 ale odjelas 4?

zad nie dajace mi spokoju: i ten wykres jednak moglabys narysowac? bo chcialabym sie upewnic lubie byc pewna na 100%

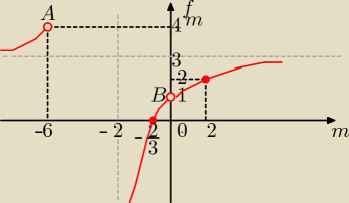
Ezop: ciężko jest tu rysować hiperbolę sorry za ten "koślawy" wykres narysuj ją sobie ładnie oznaczając jednostki na osiach odpowiadam na zadane pytanie: przekształcam do postaci kanonicznej , bo wyraźnie widać współrzędne wektora przesunięcia podstawowego wykresu u=[ −2,3] asymptoty: y= 3 i x = −2 ponad to :

	4
f(−6)=3−		=4 −−− A( −6,4)nie należy do wykresu bo m= −6 nie należy do Df
	−6+2

	4
f(0) = 3−		= 1 −−− B(0,1) też nie należy do wykresu
	0+2

	4
f(2) = 3−		= 2 −−− należy do wykresu
	4

możesz znaleźć jeszcze kilka innych punktów wówczas wykres będzie jeszcze bardziej czytelny oraz miejsce zerowe f(m) = 3m+2=0 => m= −²₃ powodzenia

zad nie dajace mi spokoju: czyli dobrze zrobilam dziekuje za szczegolowe wyjasnienia takie rozwiazywanie zadan powinno sie chwalic