Objętość ostroslupa, odleglosci od sciany bocznej i krawędzi
Ith: Witam, mam wrażenie, że umyka mi jakiś banał, przez co nie mogę tego ruszyć, będę wdzięczna za
pomoc.
Obliczyć objętość prawidłowego ostroslupa trójkątnego, znając odległości m i n środka wysokości
ostrosłupa od odpowiednio ściany bocznej i krawędzi bocznej.
1 kwi 10:40
yht:
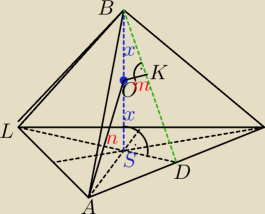
|OK| = m
|AO| = n
a − krawędź podstawy ostrosłupa
Z pitagorasa w trójkącie OSA uzależniamy x od n i a:
wstawiamy to do trójkąta BOK
OK
2+BK
2 = BO
2
m
2+BK
2=x
2
wyliczamy z tego BK
i z podobieństwa ΔBOK∼ΔBSD staramy się ułożyć proporcję z której uzależnimy a (krawędź podstawy
ostrosłupa) od m i n
1 kwi 11:03
Ith: Zaraz, a czy odległość n, nie powinna być pod kątem prostym do krawędzi, zamiast być
poprowadzoną do wierzchołka?
1 kwi 11:34
Jerzy:
Do krawędzi bocznej.
1 kwi 11:36
Ith: W takim razie dalej jestem w kropce. No chyba, że m jest przy okazji promieniem kuli.
1 kwi 11:44
Mila:
Jeśli masz odpowiedź to podaj, obliczyłam.
1 kwi 17:12
Ith: Mam:
V=18[(m3*n3)/(n2m2)√4m2−n2]
1 kwi 17:17
Mila:
Tam w mianowniku ma być: (n2−m2)*√4m2−n2
Wszystko pisać, czy tylko wskazówki?.
1 kwi 17:27
Ith: Tak, zgadza się, mój błąd.
Myślę, że wskazówki wystarczą, to sobie pokombinuję.
1 kwi 17:31
Mila:
Piszę.
1 kwi 17:34
Mila:
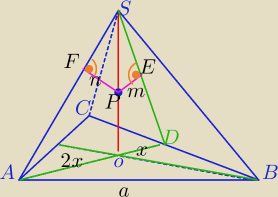
|OS|=H
1)
| | a√3 | |
|AD|=3x i |AD|= |
| ⇔a=2√3x |
| | 2 | |
V=x
2√3*H
2)
|AS|=
√H2+4x2, |DS|=
√H2+x2
3)
ΔSEP∼ΔSOD
ΔSFP∼ΔSOA
Napisz proporcje z odcinkami : m,|PS| i odpowiednikami z drugiego Δ
oraz: n , |PS| i odpowiednikami z drugiego Δ
4) oblicz x
2 i H
2
5) podstaw do wzoru z (1) wyjdzie jak trzeba:
Powodzenia. Napisz jak Ci poszło.

1 kwi 17:50
Ith: Krew, pot i łzy, ale poszło.
Bardzo, bardzo dziękuję

1 kwi 18:17
Mila:
O, to bardzo szybko! Gratuluję.

1 kwi 18:20
Mila:
Im więcej teraz potu, tym mniej krwi będzie w boju

( Powiedzonko dziadka − żołnierza)
1 kwi 18:23
Ith: Dziadek ma dużo racji

1 kwi 19:45
Ith: Jeszcze raz dzięki ^^
1 kwi 19:45
 |OK| = m
|AO| = n
a − krawędź podstawy ostrosłupa
|OK| = m
|AO| = n
a − krawędź podstawy ostrosłupa
 |OS|=H
1)
|OS|=H
1)



 ( Powiedzonko dziadka − żołnierza)
( Powiedzonko dziadka − żołnierza)
