| r | r | r | r | |||||
Zaznacz na osi przedzialy (a− | ,a+ | ) i (b− | , b+ | ) | ||||
| 3 | 3 | 3 | 3 |
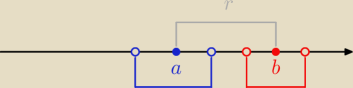 r to odległość od a do b
zaznaczyłem jakiś punkt a, b
niebieski to 1 przedział, czerwony to drugi
r to odległość od a do b
zaznaczyłem jakiś punkt a, b
niebieski to 1 przedział, czerwony to drugi
 To bylo takie cwiczenie w ksiazce
Zaraz po tym mam tw ze zaden ciag nie moze miec dwoch dowolnych granic
Dowod niech an→a i an→b Mam byc ze a=b
r− to odleglosc dwoch licz a i b (tak jak napisales
Teraz a ≠b i r≠0
Przedzialy (a−U{r/3}; a+r/3) oraz (b−r/3; b+r/3) sa rozlaczne wiec najwyzej jeden z nich moze
zawierac prawie wszystkie wyrazy ciagu an
Cwiczenie
Wyjasnij sens ostatniego zdania dowdu tego twierdzenia (mozesz dopomoc sobie rysunkiem
czy to jest w ogole potrzebne (oprocz studoiw matematycznych ?
To bylo takie cwiczenie w ksiazce
Zaraz po tym mam tw ze zaden ciag nie moze miec dwoch dowolnych granic
Dowod niech an→a i an→b Mam byc ze a=b
r− to odleglosc dwoch licz a i b (tak jak napisales
Teraz a ≠b i r≠0
Przedzialy (a−U{r/3}; a+r/3) oraz (b−r/3; b+r/3) sa rozlaczne wiec najwyzej jeden z nich moze
zawierac prawie wszystkie wyrazy ciagu an
Cwiczenie
Wyjasnij sens ostatniego zdania dowdu tego twierdzenia (mozesz dopomoc sobie rysunkiem
czy to jest w ogole potrzebne (oprocz studoiw matematycznych ?