sterometria krystek: W ostrosłupie prawidłowym trójkątnym ABCS o podstawie ABC wysokość jest równa 3, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę 120 ∘ . Oblicz objętość tego ostrosłupa Proszę o rospisanie tego bo n9ie mam pomysłu jak obliczyć krawędz podstawy .Z góry dziękuję

Rafal: https://www.geogebra.org/o/QT5VhCVT Zauważmy najpierw, że znamy długość wysokości SS', a długość odcinka S'S'' możemy szybko uzależnić od długości krawędzi podstawy, oznaczmy ją przez a. Trójkąt SS'S'' jest prostokątny, więc jeśli uzależnimy długość odcinka SS'' od a, to będzie po zadaniu, bo znamy przecież coś takiego jak twierdzenie Pitagorasa. Tak więc jedziemy z tym: 1) Ponieważ nasz ostrosłup jest prawidłowy, więc ten kąt o którym mowa znajduje się pomiędzy wysokościami ścian bocznych, które "spotykają" się na prostej zawierającej wspólną krawędź tych ścian. W tym przypadku ściany boczne okazują się być trójkątami rozwartokątnymi, więc te wysokości lądują na przedłużeniu tej krawędzi. Patrząc na trójkąt AD'D łatwo dostrzec, że

	a		a
AD'=		, a ze związków miarowych w trójkątach 90,30,60 mamy, że AD=		.
	2		√3

2) Jak teraz sprawnie policzyć długość wysokości SS''? Spoglądając na trójkąt CAD widzimy, że

	1
sinγ=		i ten kąt o mierze γ musi być ostry, bo leży przy podstawie trójkąta
	√3

	√6
równoramiennego CAS, więc cosγ>0, co oznacza, że cosγ=		(jedynka trygonometryczna), a
	3

	√2		a√2
co ca tym idzie tgγ=		(bo tgx=sins/cosx). Stąd wiemy, że SS''=		(bo
	2		4

	a
CS''=		).
	2

	a√2		a√3
3) Z twierdzenia Pitagorasa (		)2=9+(		)2 ⇒ a=6√6.
	4		6

undefined

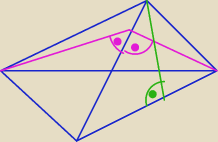
Rafal: Tak naprawdę przy rysowaniu rysunku możesz roboczo założyć, że te wysokości spotykają się na krawędzi, a nie na jej przedłużeniu. To rozumowanie także wówczas zadziała. undefined