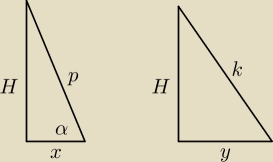ostrosłup mały: W ostrosłupie prawidłowym trójkątnym ściana boczna jest nachylona do płaszczyzny podstawy pod katem 30 stopni i krawędzie boczne mają długość √13 .Oblicz objętość i pole całkowite tego ostrosłupa Bardzo proszę o pomoc

Jerzy: p − wysokość ściany bocznej k − krawędź

	1
x =		h ( h − wysokość podstawy )
	3

	2
y =		h
	3

	a√3
h =
	2

a − krawędź podstawy

	1	a2√3
V =			*H
	3	4

Musisz obliczyć: a i H

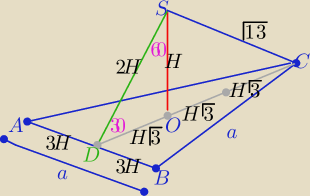Eta: Wprowadzam oznaczenia zgodnie z własnościami "trójkąta ekierki"(30^o,60^o,90^o) a=6H , h_p=3H√3 Z tw. Pitagorasa w ΔOCS: H²+(2H√3)²=(√13)² ⇒ 13H²=13 ⇒ H=1

	1
Pp=		*6H*3H√3=9H2√3 =9√3 [j3]
	2

	1
V=		*Pp*H=3√3
	3

	1
Pc= Pp+3*		*6H*2H= 9√3+18 =9(√3+2) [j2]
	2

i po bólu

Jerzy: Awesome

5-latek: Dobry wieczor Pozdrawiam Ale to jest mały ból A jak bedzie duzo wiekszy to jak napiszesz? duży b..l