Oblicz długości środkowych trójkąta. Majka: Pole trójkąta prostokątnego ABC jest równe 6√3. Wysokość opuszczona z wierzchołka kąta prostego dzieli kąt prosty w stosunku 1:2. Obliczyć długości środkowych, wychodzących z wierzchołków ostrych tego trójkąta.

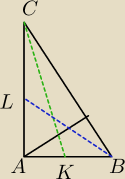
Jerzy: IBCI = a

	1
IABI =		a
	2

IACI = a√3 Z pola trójkata obliczasz a = 2√6

	1
ICKI2 + (		a)2 = (a√3)2
	4

	1		1	a√3
IBLI2 = (		a)2 + (			)2
	2		2	2

Eta:

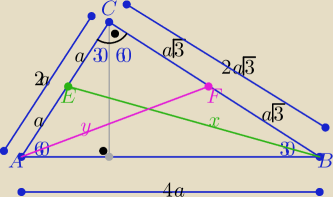
	1
P(ABC)=		*|AC|*|BC| =6√3 ⇒ a=√6
	2

z tw. Pitagorasa w trójkątach AFC i BEC y²=(2a)²+(a√3)² x²=a²+(2a√3)² y²=7a²=42 x²=13a²=78 y=........... x=.......

Majka: Eta wkradł się błąd, a wychodzi 2√6, Jerzy pierwszy Pitagoras chyba źle, ale dzięki wielkie, nie mogłam wpaść na pomysł a dzięki Wam rozwiązane, pozdrawiam

Majka: *poprawka, Eta: przy Twoich oznaczeniach a wychodzi √3 a Jerzy IACI wychodzi a√3/2, stąd błąd w Pitagorasie, poprawcie mnie jeśli się mylę? Bo już się nie mogę odnaleźć w tym bałaganie

Jerzy: Pomyłka jest u mnie:

	a√3
|AC| =		, a nie : a√3
	2

Majka: oki, to już wszystko jasne, dzięki!