wielomian Gucio18: Wielomian W(x)=x³−3x²−x+3 ma 3 pierwiastki całkowite.Wykaż że jeżeli P(X)=W(x)+x+2 to wielomian P ma tylko 1 pierwiastek

kochanus_niepospolitus: W(x) = (x−3)(x−1)(x+1) <−−− skoro było podane że pierwiastki są całkowite, to trza było spojrzeć na dzielniki wyrazu wolnego P(x) = (x² − 4x + 3)(x+1) + (x+2) P(x) = (x² − 4x + 3)(x+1) + (x+1) + 1 P(x) = (x² −4x + 4)(x+1) + 1 P(x) = (x−2)²(x+1) + 1

	1
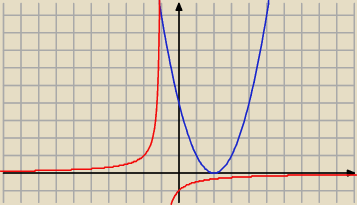
P(x) = 0 ⇔ (x−2)2(x+1) = −1 ⇔ (x−2)2 = −
	x+1

rysujemy wykres f(x) = (x−2)² i widzimy, że tylko jeden punkt przecięcia jest z funkcją

	1
g(x) = −
	x+1