podobieństwo cotyniepowiesz98: Wewnątrz trójkąta ABC obrano punkt P tak, że kąt CAP = kąt CBP. Uzasadnij, że trójkąt APL ~ trójkąta BPK oraz trójkąt APB~trójkąt KLP , gdzie punkty K i L są punktami przecięcia prostych AP i BP odpowiednio z bokami BC i AC. Pierwsze podobieństwo bez problemu (kkk) Ale z drugim nie do końca mi wychodzi... Czy AB jest równoległa do KL

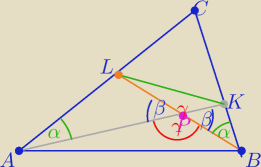
Eta: 1/ ΔAPL∼ΔBPK z cechy (kkk) 2 / ΔAPB ∼ΔKLP z cechy (b,k,b)

	|AP|		|PL|
bo mają boki proporcjonalne z (1)		=
	|BP|		|PK|

i kąt wspólny między nimi γ i to wszystko