Wielomian trzeciego stopnia z parametrem asurbanipal: Dana jest funkcja f(x) = m³ − 3x² + 3mx + 1. Funkcja g(m) przypisuje każdej wartości parametru m liczbę ekstremów, jaką ma funkcja f dla tego parametru m. Wyznacz wzór oraz naszkicuj wykres funkcji g.

Jerzy: Na początku nie ma aby nawiasu ?

asurbanipal: Nie, ale jest mx³ f(x) = mx³−3x²+3mx+1

hc44rs99:

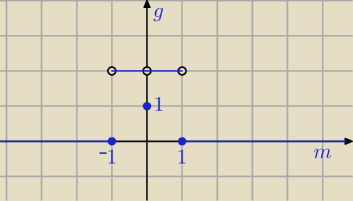
piotr: dla m=0 jedno ekstremum, bo f. kwadratowa dla m≠0 Funkcja traciego stopnia (może mieć 0 lub 2 ekstrema) f'(x) = 3mx²−6x+3m mx² − 2x + m = 0 2 ekstrema dla Δ=4−4m²>0 ⇒ −1<m<1 ∧ m≠0 0 ekstremów dla pozostałych