Prawdopodobieństwo zagubiony: Ze zbioru wierzchołków pewnego ośmiokąta foremnego losujemy trzy punkty. Rozpatrzmy następujące zdarzenia losowe: A − wylosowane punkty są wierzchołkami trójkąta równoramiennego, B − wylosowane punkty są wierzchołkami trójkąta prostokątnego, C − wylosowane punkty są wierzchołkami trójkąta rozwartokątnego. Obliczyć prawdopodobieństwa zdarzeń A, B, C oraz rozstrzygnąć, czy zdarzenia A i B są niezależne.

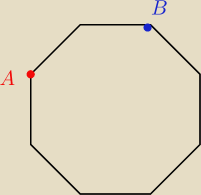
kochanus_niepospolitus: a) wybieramy wierzchołek A (na 8 sposobów) wybieramy wierzchołek B (na 7 sposobów −−− w różnych wariantach) wybieramy wierzchołek C (w różnych wariantach) a1) wierzchołek B jest 'odległy' od A o '2 lub 4 boki' (czyli mamy na 3 sposoby) wtedy wierzchołek C wybieramy także na 3 sposoby a2) wierzchołek B jest 'odległy' od A o '1 lub 3 boki' (czyli mamy 4 sposoby) wtedy wierzchołek C wybieramy także na 2 sposoby

	8*(3*3 + 4*2)
P(A) =
	8*7*6

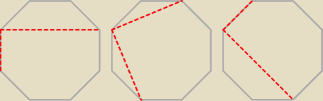kochanus_niepospolitus: b) wierzchołek A na 8 sposobów dla każdego wierzchołka będą 3 trójkąty prostokątne (gdzie kąt prosty jest przy tym wierzchołku)

	8*3		1
P(B) =		=
	8*7*6		14

zagubiony: Bardzo dziękuje! Ma Pan pomysł na podpunkt c)?

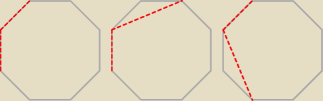kochanus_niepospolitus: jedynie te trzy trójkąty będą istniały, tak aby w pokazanym wierzchołku był kąt rozwarty.