Wykaż (prawdopodobieństwo) Mleko: A oraz B są zdarzeniami losowymi zawartymi w Ω. Wykaż, że jeżeli P(A)=0,9 i P(B')=0,8, to P(A\B)≥0,5 Wiemy, że P(B)=0,2 i nie wiem co dalej

Alky: Wiemy też, że P(A)−P(AnB)=0,8 P(AnB)=0,1 Wzór i jesteśmy w domu

Mleko: Dzieki

Mleko: A czy można tego nie obliczać, ale jakoś pokazać, że rzeczywiście P(A\B)≥0,5 ?

Alky: Hm, wydaje mi się, że trzeba skorzystać, ze wzoru na prawdopodobieństwo warunkowe, do którego wszystko w sumie mamy podane, praktycznie nic nie trzeba wyliczać, tylko coś przekształcić/zauważyć. Ja bym to robił tak. Nic mi teraz nie przychodzi innego do głowy, ale to nie znaczy, że to jedyny sposób. Może ktoś bardziej doświadczony się wypowie, choć nie iwem czy jeszcze tej nocy

Pytający: Alky, nie wiem, skąd wytrzasnąłeś zależność P(A)−P(AnB)=0,8... P(A\B)=P(A∩B') Mamy: P(A∪B')=P(A)+P(B')−P(A∩B')=0,9+0,8−P(A∩B')=1,7−P(A∩B')≤1 ⇒ P(A∩B')≥0,7

Alky: B'=A−A∩B Zbiory nie są rozłączne więc z prawdopodobieństwami zachodzi to chyba tak samo. Mogę się jedank mylić, bo z prawdopodobieństwa orłem nie jestem i niespecjalnie to lubię. Jeśli rzeczywiście się mylę to wytłumaczysz mi na czym polega mój błąd bo nie rozumiem Może i ja się czegoś nauczę ^^

Alky: Jeśli jest źle to mogę przedstwić w pełni swój... tok rozumowania i mnie naprowadzisz na dobrą drogę

Alky: Generalnie, na moje P(B')=P(A)−P(A∩B) P(B')=0,8 , więc i P(A)−P(A∩B)=0,8 Jak mówiłem, prawdopodobieństwo nie jest moją mocną stroną, więc uparcie nie będę się trzymał swojego, ale musi mi ktoś powiedzieć co robię źle ( o ile robię ), bo inaczej nie zasnę Dalej zadanie bym robił tak: 0,9−P(A∩B)=0,8 P(A∩B)=0,1

	(A∩B)		0,1
P(A\B)=		=		=0,5 w sumie teżby się zgadzało co do zadania .
	P(B)		0,2

Pytający: 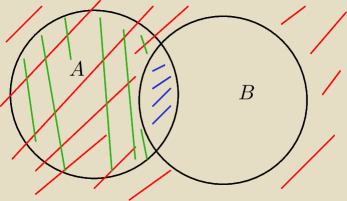B' A∩B A−A∩B Już widać, że niekoniecznie B'=A−A∩B (niekoniecznie, bo może się tak zdarzyć, ale nie jest to jakaś zasada)?

Pytający: A tak poza tym to P(A\B)≠P(A|B). P(A\B)=P(A)−P(A∩B)=P(A∩B')

	P(A∩B)
P(A|B)=
	P(B)

Alky: Okej przetrawiłem. Oczywiście masz racje. Nie wiem czemu uznałem, że P(AUB)=1 Tak jakbym założył, że AuB dają razem Ω Eh. No dowodzi to tylko tego, że jeszcze mi .. troszke.. brakuje z tego prawdopodobieństwa. Dzięki. Teraz będę mógł się spokojnie położyć spać