Wykres funkcji homograficznej Kamil:

	ax + b
Na rysunku obok przedstawiony jest wykres funkcji homograficznej F(x) =		,
	x + b

gdzie x≠−b i ab−b≠0. Korzystając z tego rysunku oraz wiedząc że do wykresu funkcji F należy punkt A(1, −1), wyznacz wzór funkcji F. Następnie naszkicuj wykres funkcji G(x) = F( lxl ) i

	m + 3
ustal, dla jakich wartości parametru m ( m∊R ) równanie G(x) =		nie ma
	m

rozwiązań. tutaj zdjęcie rysunku: http://scr.hu/2yfp/0kbqf Wyznaczyłem sobie wzór funkcji, ale mam problem ze sporządzeniem wykresu G( x ), czy mógłby ktoś wytłumaczyć jak go wykonać?

Tadeusz:

	4
f(x)=		+3
	x−2

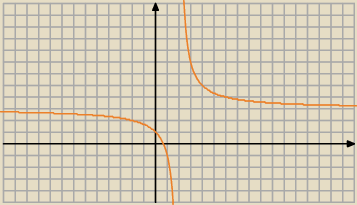
g(x)=f(|x|) rysujesz tak, że dla dodatnich x bez zmian a dla ujemnych odbicie względem Oy To jest wykres f(x)

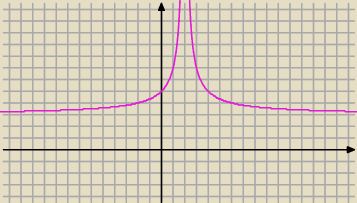
Tadeusz: a to f(|x|)

Kamil: w odpowiedziach jest tak: https://pl-static.z-dn.net/files/d43/a11430ed6ed4c35f302abc3b25758996.jpg znalazłem w internecie

Tadeusz: oczywiście ... w kreatorze wykresu "nie weszła" dolna część

Kamil: tą część którą wstawiłeś rozumiem, ale skąd się bierze ta dolna część? i dlaczego ten wykres Twój jest narysowany względem przesuniętego układu współrzędnych, a ten z odpowiedzi jest narysowany względem normalnego, nieprzesuniętego układu współrzędnych? może to są oczywiste rzeczy, ale tego nie rozumiem więc przepraszam za niewiedzę

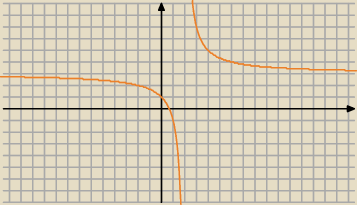
Tadeusz: to jest

	4
f(x)=		+3
	x−2

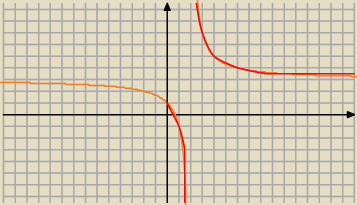
Tadeusz: rysując f(|x|) bez zmian pozostaje to co jest po prawej stronie 0y

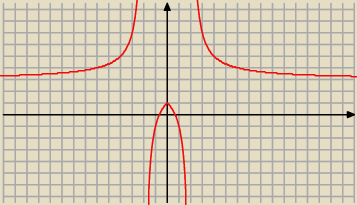
Tadeusz: a na lewej stronie "lustro" prawej strony 0y

Tadeusz:

	m+3
i teraz ten ostatni wykres "kroisz" stałą y=
	m

Kamil: już rozumiem, dzięki wielkie za pomoc!

Tadeusz: duży rośnij

Kamil: a jeszcze jedno, tym sposobem robiłem kolejne zadanie z wykresem wartości bezwzględnej i rysuje to w ten sposób: http://scr.hu/2yfp/fv50c a w odpowiedziach jest zupełnie inaczej: http://scr.hu/2yfp/dtddi co robię źle?

5-latek: To nie jest to samo f(x)= U{|x|}{x−1| dla x≠1

	x
rozpatrujesz dwa przypadki x≥0 to |x|= x ⇒f(x)=		= itd
	x−1

	−x
dla x<0 |x|= −x to f(x)=		= itd
	x−1

Kamil: spróbowałem tym sposobem i dochodzę do tego momentu: http://scr.hu/2yfp/qb7yl i nie wiem z czego wynika ta część od zera w dół widoczna w odpowiedzi? mógłby mi ktoś to wyjaśnić?