Planimetria Dominik: Sposoby na planimetrie, dowody itp. Witam mam dosyć spory problem, otóż zupełnie nie wychodzą mi zadania z planimetrii. Nie umiem ich robić, zabrać się za nie, nie widzę istotnych rzeczy itp. Oczywiście ćwiczę jak najwięcej się da ale jutro piszemy sprawdzian a ja po przerobieniu około 200 zadań w niecałe 2 tygodnie nie umiem praktycznie nic. Jakie macie sposoby, magiczne rozwiązania do większości zadań z planimetrii a szczególnie tych dowodowych? Pewnie naiwnie myślę, że coś takiego jest bo jestem serio tym załamany..

Antonni: Nie przejmuj sie tym , Nie tylko Ty tak myslisz (tzn naiwnie

Dominik: Pocieszające..

'Leszek: Przede wszystkim w planimetrii w figurze szukaj trojkatow i korzystaj z wlasnosci trojkatow np. sumy katow ,funkcji trygonometrycznych katow, tw. Pitagorasa.... Czasami musisz metoda prob i bledow sprawdzic jakie wlasnosci trzeba w danym zadaniu wykorzystac , nie ma innej rady , naogol nie ma duzo opcji .Powodzenia !

Alky: Nie wiem co jest dziwniejsze − to, że robiłeś ( wg tego co mówisz ) średnio 14 zdań z planimetrii dziennie i nie umarłeś, czy to że po zrobieniu 200 z tego zakresu dalej nic nie umiesz...

Dominik: 200zadan dla mnie to duzo, zazwyczaj po o wiele mniejszej ilosci juz potrafie o wiele wiecej. Nie doslownie nic nie umiem tylko bardziej chodzi o to ze w wielu zadaniach nadal nie wiem co mam zrobic, i chcialbym wymagac od siebie wiecej aby to po prostu umiec..

'Leszek: To zrob nastepujace zadanie : W Δ ABC kat ABC = 120 ° , oraz | AB | = √3 i | BC | = √12 , obliczyc odcinek dwusiecznej kata ABC zawartej w Δ .

Dominik: Wyszło mi ^2√6_√6+√2 co jest pewnie błednym wynikiem... Zajęło mi to jedynie 19minut a na sprawdzianie ma być ok. 6 zadań

Dominik: ten √2 tez w mianowniku

'Leszek: Niech punkt D oznacz punkt przeciecia dwusiecznej z bokiem AC. x − dlugosc dwusiecznej AD = x Pole Δ ABC = 0,5 √3 *√12 sin 120 ° Pole Δ ABD = 0,5 * √3 *x sin 60 ° Pole Δ DBC = 0,5 *√12 *x sin 60 ° Pole Δ ABC = pole Δ ABD + pole Δ DBC wpisywanie mi zajelo 5 minut , a wiesz ,ze nie jest to takie szybkie jak dlugopisem na kartce papieru .

Dominik: ^{2(√12−√3)}₃ I czemu ja nie mogłem na to wpaść..

'Leszek: No to na przyszlosc bedziesz wiedzial , pisalem Ci , ze trzeba przemyslec kilka opcji i dlatego zadania z planimetrii sa nie tylko dla Ciebie trudne , ale nie zalamuj sie bedzie dobrze ,powodzenia w nauce matematyki !

Eta:

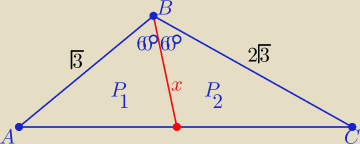
	6√3
P=P1+P2 , P=.......=
	4

	3x
P1=........=
	4

	6x
P2=.........=
	4

	2√3
9x=6√3 ⇒ x=
	3

Dominik: Przydadzą się