równanie trygonometryczne wkrotceMistrz^: Rozwiąż równanie: 12sinα=20sin3α

Janek191: 3 sin α = 5 sin 3α oraz sin 3α = 3 sin α − 4 sin³α itd.

wkrotceMistrz^: a jak doszłam już do momentu, że mam sinα=√³₅ a dalej mam wyznaczyć sin2α i nie wiem jak. bo wiem, że sin2α=2sinαcosα, ale skąd mam wziąć cosα ?

Janek191: cos² α =1 − sin²α ⇒ cos α = √ 1 − sin² α

Alky: Jedynka tryg ?

wkrotceMistrz^: z 1 trygonometrycznej cosα=√1−sin²α ? Tak ma być ?

Adamm: sinα=√3/5 ⇒ cosα=±√2/5 sin2α=±2√6/5

wkrotceMistrz^: dobra, dzięki mam, może jest jeszcze dla mnie nadzieja.

Adamm: kto wam powiedział że cosinus jest dodatni, to ja nie wiem

wkrotceMistrz^: to nie całe zadanie tylko równanie wyrwane z kontekstu, cosinus jest dodatni, bo chodzi o katy w trójkącie.

wkrotceMistrz^: niecałe*

Antonni: Tez nie bardzo bo dla kąta rozwartego cosinus jest ujemny

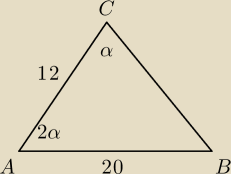
wkrotceMistrz^: Ogólnie to zdanie jest takie: dany jest trójkąt abc o bokach ab=20 i ac=12, wyznacz bok bc, wiedząc, że ∠cab=2∠acb.

wkrotceMistrz^: wydaję mi się, że jak cos będzie ujemny to wartość bc też będzie ujemna

Adamm:

	20		|BC|		|BC|
z tw. Sinusów		=		⇒ cosα=
	sinα		sin2α		40

	|BC|
z tw. Cosinusów 202=122+|BC|2−2*|BC|*12*
	40

|BC|²=640 |BC|=8√10 ok?

Adamm: cosinus wyszedł taki sam, więc raczej tak