rachunek różniczkowy Pati18773: Narysuj wykres funkcji f i wyznacz jej ekstrema. W których punktach funkcja ta nie ma pochodnej? f(x)=Ix³+3x+4I czy trzeba to rozwiązać przypadkami 1) x∊(−∞;0) 2) x∊<0;+∞) ?

Jerzy: Narysować wykres x³ + 3x + 4 i odbić to co pod osią OX nad oś.

Janek191: Rozłóż x³ +3 x + 4 na czynniki f(−1) = 0

Pati18773: i potem ekstrema tez odbić ?

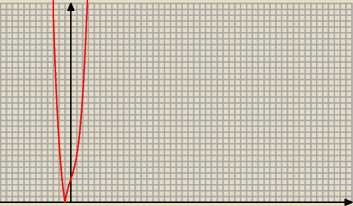
Adamm: minimum lokalne w punkcie x=−1

Pati18773: wyszło mi że x³+3x+4=(x²−x+4)(x+1)

Pati18773: i mam teraz obliczyć pochodną tego ?

Adamm: tak

Pati18773: wyszło 3x²+3 warunek konieczny to ze to musi sie równać 0

Jerzy: Pochodna jest stale dodatnia, a więc funkcja ( pod wart. bezwzgl.) stale rośnie.

Pati18773: nie wiem co mam dalej z tym zrobić

Jerzy: Zatem wyznaczasz x , dla którego wykres przecina oś OX i to jest szukane minimum.

Pati18773: wychodzi że x²=−1

Adamm: teraz wyznacz pochodną dla funkcji f(x)=|x³+3x+4|

Jerzy: Co za bzdury wypisujesz ? (x² − x +4)(x +1) = 0 ⇔ ?

Pati18773: ale jak bo nie wiem tego

Pati18773: przyrównałam pochodną do 0 3x²+3=0

Jerzy: A po co ?

Pati18773: no warunek konieczny aby wyznaczyć ekstrema

Pati18773: to czemu (x²−x+4)(x+1)=0 ?

Jerzy: Przecież od razu widać,że pochodna jest zawsze dodatnia.

Jerzy: To nie jest pochodna , tylko funkcja rozłożona na czynniki.

Pati18773: to dlatego (x²−x+4)(x+1)=0 ?

Jerzy: Z tego równania obliczysz miejsce zerowe funkcji.

Pati18773: no tak

Jerzy: W takim razie funkcja wyjściowa osiąga minimum dla: x = −1 i wynosi ono 0

Pati18773: dobra a jak z tym że ona przechodzi przez 4

Jerzy: f(0) = ?

Pati18773: no tak to widzę tylko mam to po prostu napisać że f(0)=4 czy rozpisać jakoś ?

Jerzy: Liczę punkt przecięcia wykresu z osią OY: f(0) = |4| = 4 , zatem P(0,4)

Pati18773: trochę dziwne to zadanie inne przykładny to tak rachunkowo mi wyszło a to takie bardziej na wyobrażenie sobie