oblicz pole trójkątów kacper: W trójkąt prostokątny wpisano okrąg o promieniu r=5. Cosinus kąta ABC wynosi 0,8. Punkt D jest punktem styczności okręgu z przeciw prostokątną AB. Oblicz pole trójkątów ADC i DBC.

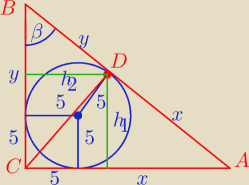
Janek191: x > 5 Mamy

	y + 5
cos β =		= 0,8 ⇒ y + 5 = 0,8 x + 0,8 y ⇒ 0,2 y = 0,8 x − 5 / * 5
	x + y

y = 4 x − 25 oraz ( 5 + x)² + ( 5 + y)² = ( x + y)² 25 + 10 x + x² + ( 4 x − 20)² = ( 5 x − 25)² 25 + 10 x + x² + 16 x² − 160 x + 400 = 25 x² − 250 x + 625 8 x² − 100 x + 200 = 0 / : 4 2 x² − 25 x + 50 = 0 Δ = 625 − 4*2*50 = 625 − 400 = 225 √Δ = 15

	25 − 15
x =		= 2,5 − odpada
	4

lub x = 10 y = 15 Oblicz wysokości trójkątów a następnie ich pola.

Janek191: Mamy

	5 + y		20
U{h1}[x} =		=
	x + y		25

h1		4
	=		/ * 10
10		5

h₁ = 8 więc pole Δ ADC P₁ = 0,5*15*8 = 60 [j²} Pole Δ ABC P = 0,5*15*20 = 150 [j²] Pole Δ DBC P₂ = P − P₁ = 150 − 60 = 90 [j²]