ciąg art. ciąg geomeryczny, wykaż że to trójkąt równoboczny denzel: Wyjaż, że trójkąt którego miary kątów tworzą ciąg artmetyczny a długości boków są wyrazami ciągu geometrycznego , jest trójkątem równobocznym.

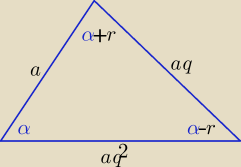
Eta: 1/ α+α+r+α−r=180^o ⇒ α=60^o 2/ z tw. kosinusów a²q²=a²+a²q⁴−2*a*aq²*cos60^o /: a>0 i q>0 q²=1+q⁴−q² ⇒ q⁴−2q²+1=0 ⇒(q²−1)²=0 ⇒ q=1 −− ciąg stały to boki maja równą długość "a" zatem taki trójkąt jest równoboczny

denzel: dzięki, mam pytanie tylko dotyczące kątu alfa − r, dlaczego minus? skoro ciąg art. to a1+ (n−1)r

Eta: a, a+r, a+2r ja wolę taki zapis : a−r, a, a+r

denzel: już to ogarnąłem dzięki jeszcze raz za pomoc

Eta: Na zdrowie......