Mam napisac rownanie plaszczyzny przechodzacej przez dwie proste Twix: Mam napisac rownanie plaszczyzny przechodzacej przez proste:

	⎧	x=2+t
l1:	⎨	y=−1+2t
	⎩	z=1−t

	⎧	x=2s
l2:	⎨	y=4s
	⎩	z=−2s

Obliczam: P1 = (2,−1,1) P2=(0,0,0) |v| = [1,2,−1] i teraz tutaj moje pytanie − Daczego liczymy iloczyn wektorowy w tym przykladzie akurat w taki sposob: v x P1P2 , a nie na odwrot (P1P2 x v) i od czego to zalezy? V x P1P2 = (−1,3,5) A(x−x0)+B(y−y0)+C(z−z0)=0 −1(x−2)+3(y+1)+5(z−1) −x+3y+5z=0

Twix: A w tym przykladzie:

	⎧	x=2+t
P=(2,−1,0) l:	⎨	y=−1+2t
	⎩	z=1−t

v=[1,2,−1] P0 = (2,−1,1) P0P = (0,0,−1) i tutaj liczymy P0P x V a nie odwrotnie, dlaczego?

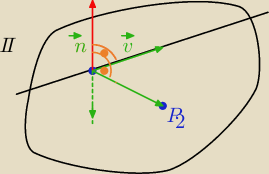
Mila: To jest obojętne; Otrzymałeś równanie płaszczyzny: −x+3y+5z=0 /*(−1) π: x−3y−5z=0 2) P₁P₂^→ x v^→=[1,−3,−5] wektor prostopadły. do płaszczyzny π, jest to wektor o przeciwnym kierunku do poprzedniego. 3) Napiszmy równanie płaszczyzny: P1 = (2,−1,1)∊π 1*(x−2)−3(y+1)−5*(z−1)=0 x−2−3y−3−5z+5=0 π: x−3y−5z=0

Mila: W pierwszym przykładzie proste są równoległe, a w drugim?