pytanie. Lubięliczyć: http://scr.hu/0t2s/d3it3 −−−> Będą się przecinać kiedy a=0 lub −2<ax<1 ?

kochanus_niepospolitus:

	−3
x+1 = ax−2 ⇔ x(1−a) = −3 ⇔ (dla a≠1) x =		< 0 ⇔ 1−a > 0
	1−a

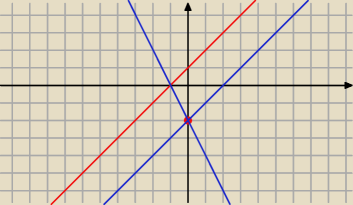
Adamm: a∊(−2;1)

kochanus_niepospolitus: o obu ujemnych no to jeszcze y=x+1 < 0 −> x>1 i robimy część wspólną

Lubięliczyć: Ok spoko, ale co z warunkiem a>−2? Odpowiedz jest jasna wynikająca z rysunku Adama, niestety nie mogę dojść do tego warunku.

Adamm:

	−3
f(x)=g(x) ⇒ x+1=ax−2 ⇒ (a−1)x=−3 ⇒ x=
	a−1

tak jak wspomniał kochanus, y<0 oraz x<0

	−3		−3
zatem		+1<0 oraz		<0 co trzeba rozwiązać
	a−1		a−1

Lubięliczyć: Dziękuję.