| 24√2 | ||
przecięła przeciwwprostokątną w punkcie D.Wykaż,że długoścć AD= | .Długosci | |
| 7 |
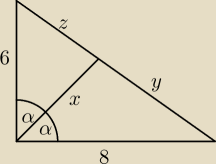 skorzystaj z tw. o dwusiecznej w trójkącie: https://matematykaszkolna.pl/strona/498.html
zauważ, że y+z = 10 (patrz trójkąt prostokątny i tw. Pitagorasa)
wyznacz y i z
z któregoś z nich liczysz z tw. cosinusów i wyznaczasz 'x'
skorzystaj z tw. o dwusiecznej w trójkącie: https://matematykaszkolna.pl/strona/498.html
zauważ, że y+z = 10 (patrz trójkąt prostokątny i tw. Pitagorasa)
wyznacz y i z
z któregoś z nich liczysz z tw. cosinusów i wyznaczasz 'x'
| z | y | |||
Czy aby na pewno wystarczy samo to twierdzenie ? ( | = | ) | ||
| 6 | 8 |

 Super,dziekuję
Super,dziekuję
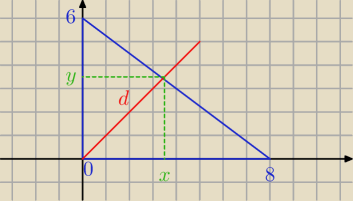
| 0 − 6 | 3 | |||
a = | = − | |||
| 8 − 0 | 4 |
| 3 | ||
y = − | x + 6 | |
| 4 |
| 3 | ||
x = − | x + 6 / * 4 | |
| 4 |
| 24 | 576 | |||
x = | ⇒ x2 = | |||
| 7 | 49 |
| 24 | 576 | |||
y = | ⇒ y2 = | |||
| 7 | 49 |
| 24√2 | ||
d = √ 115249 = | ||
| 7 |


 Janek dziekuję .Jedno zadanie a tyle rozwiązań.To wspaniałe,że istnieje to forum
Janek dziekuję .Jedno zadanie a tyle rozwiązań.To wspaniałe,że istnieje to forum
 Krótko i na temat
Krótko i na temat 
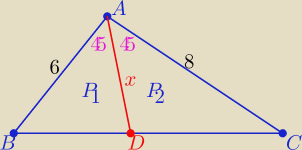
| √2 | √2 | |||
P(ABC)=P=24 , P1=3x*sin45o= 3x* | , P2=4*x*sin45o=4x | |||
| 2 | 2 |
| √2 | 24√2 | |||
P1+P2=7x* | to P=P1+P2 ⇒ 7x√2=48 ⇒ x= | |||
| 2 | 7 |
