TRYGONOMETRIA nowy: Cześć mam problem, pomożecie?

	√6+√2		√6−√2
Punkt P(		,		) leży na ramieniu końcowym kąta 15 stopni. Oblicz
	4		4

sin α i cosinus α, jeżeli: α= 165 stopni

johny: a co udało Ci się określić?

nowy: Właściwie to wiem tylko że punkt leży w pierwszej ćwiartce i nie wiem jak sobie z tym poradzić. Ponieważ nie wiem pomiędzy czym jest te kąt alfa

Janek191: 165^o = 180^o − 15^o i wzory redukcyjne.

nowy: a mógłbyś rozpisać do końca?

nowy: bo 165 stopni mam tutaj rozumieć jako odchylenie tego ramienia o 165 stopni od tych 15 czy od początku?

Janek191:

	√6 − √2		√2 − √6
sin ( 165o) = sin( 180o − 15o) = − sin 15o = −		=
	4		4

Janek191: Podobnie z kosinusem

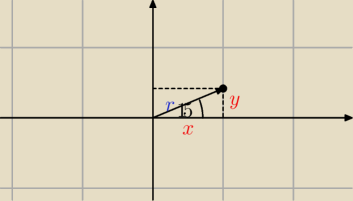
Antonni: r=√x²+y²

	y
sin15o=
	r

	x
cos15o=
	r

Teraz to prosze policzyc

	√6+√2
x=
	4

	√6−√2
y=
	4

Potem wzory redukcyjne .

nowy: A o to chodzi rozumiem, dzięki. Ja policzyłem r już wcześniej, ale nie wiem jakoś nie wpadłem na to

Antonni: Chociaz powinno wyjsc r=1 Zauwaz (ja tez to dopiero zauwazylem) ze mamy podane wspolrzedne punktu ktire leza na koncowym ramieniu kąta wiec ten kat jest jednoznacznie okreslony My nie musimy liczyc wartosci kąta majac punkt tylko mamy dana juz miare kąta . Wspanialomyslny autor zadania