Granice+ ciagi
Fanabela: Wyznacz dziedzine funkcji f, określ jej najmniejszą wartość oraz naszkicuj wykres, jeśli:
f(x)=lim
n→∞ (1+ x
2+ x
4+... x
2n)
To w nawiasie oznaczylam jako g(x) ( jest to ciąg geometryczny ⇒ a
1=1 i q=x
2)
Zatem g(x)={1−x
2n}{1−x
2} i wyznaczam dziedzine funkcji g⇒ x≠1 i x≠−1 i tu utknęłam,
bo w odp D=(−1,1) a wartość minimalna f(0)=1. Nie mam również pomysłu na dalsze przekształcenia
wzoru funkcji. Proszę o pomoc

27 mar 18:54
Janek191:
I q I < 1
27 mar 18:57
Fanabela: Przepraszam, wzór funkcji g(x) ( nie zrobił mi się pierwiastek)
27 mar 18:57
Fanabela: A tak racja, zapomniałam o zbieżności, a jak przekształcić ten wzór,
tak żeby można było zrobić wykres?
27 mar 18:59
Antonni: 1−x2n= (1+xn)(1−xn)
Nie wiem czy to cos pomoze
27 mar 19:02
27 mar 19:04
Janek191:
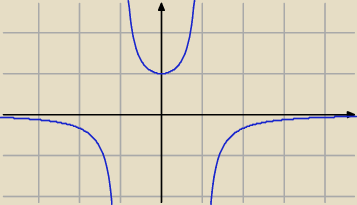
27 mar 19:05
Fanabela: Też tak robiłam mianownik i licznik, ale to chyba nie tędy droga...
27 mar 19:05
Fanabela: Ale czy jeżeli mamy teoretycznie podany ostatni wyraz ciągu to możemy to potraktować jako
szereg?
27 mar 19:06
Janek191:
n → ∞
27 mar 19:09
Fanabela: Tylko w poleceniu jest narysowanie funkcji f(x) więc jak uwglednic limn→∞ skoro n nie ma w
g(x)
(jak przyjmiemy wersje z szeregiem geometrycznym)?
27 mar 19:09

