Bryły Dawidos 345: Trzy krawędzie prostopadłościanu mają wpólny koniec. Pozostałe końce tych krawędzi wyznaczają płaszczyznę π. Wykaż że płaszczyzna ta dzieli w stosunku 1:2 przekątną prostopadłościanu wychodzącą ze wspólnego końca danych krawędzi. Proszę o rysunek kompletnie nwm jak to zrobić,a muszę to jutro zreferować przy tablicy ?

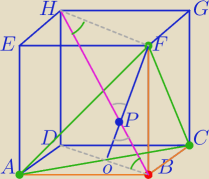
Mila: π: ΔACF BH−przekątna prostopadłościanu wychodzącą ze wspólnego końca krawędzi: BC,BA,BH P −punkt przecięcia przekątnej BH i odcinka OF ( środkowa przekroju)

	|OB|		1
ΔOBP∼ΔHFP ( cecha kkk) w skali k=		=		⇔
	|HF|		2

PB		1
	=		⇔|HP|=2|PB|
HP		2

cnw