stereometria Krakus: Podstawą ostrosłupa jest kwadrat ABCD o boku długości 40. Pola ścian bocznych ABS , BCS , CDS i ADS są odpowiednio równe: 740, 240√5 , 260 i 400. Oblicz objętość tego ostrosłupa. Proszę o pomoc

Krakus: czy mógłby ktoś napisać chociaż jak to zacząć?

Mila: Masz może odpowiedź do zadania?

Krakus: niestety nie

Mila:

	1
V=		*402*H
	3

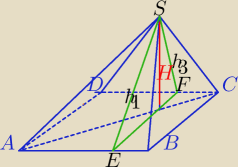
Problem polega na wyznaczeniu wysokości ostrosłupa. Trzeba poszukać przekroju w którym ta wysokość się znajduje. 1) Wyznaczymy wysokości ścian bocznych:

	1
740=		*40*h1⇔h1=37
	2

	1
240√5=		*40*h2⇔h2=12√5
	2

	260
h3=		=13
	20

	400
h4=		=20
	20

2) Spodek wysokości znajduje się bliżej punktu C Weźmy ΔEFS jako przekrój w którym znajduje się H P_ΔEFS: Boki: 37,40, 13 40²≠37²+13² nie jest to Δprostokątny,

	37+40+13
Pole z wzoru Herona: p=		=45
	2

P_ΔEFS=√45*(45−37)*(45−40)*(45−13)=15*16

	1
15*16=		*40*H
	2

H=12 3) sprawdź, czy w drugim przekroju wysokość H też będzie równa 12.

Krakus:

	24√6
w drugim H będzie
	5

Krakus: a nie przepraszam coś pomiliłem

Krakus: Dzięki wszystko się zgadza