 t = x2 ≥ 0
3 t2 − 6 t + 4 = 0
Δ = 36 − 4*3*4 = < 0 − brak miejsc zerowych wielomianu.
t = x2 ≥ 0
3 t2 − 6 t + 4 = 0
Δ = 36 − 4*3*4 = < 0 − brak miejsc zerowych wielomianu.
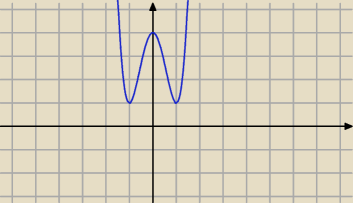
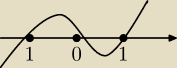 f'(x)=12x3−12x=12x(x2−1)
12x(x2−1)=0
x1=0 v x2=1 v x3=−1
f'(x)<0 x∊(−∞,−1)∪(0,1) f↘ (−∞,−1>u<0,1>
f'(x)>0 x∊(−1,0)∪(1,+∞) f↗ <−1,0>∪<1,+∞)
jak wyznaczyć fmax i fmin
f'(x)=12x3−12x=12x(x2−1)
12x(x2−1)=0
x1=0 v x2=1 v x3=−1
f'(x)<0 x∊(−∞,−1)∪(0,1) f↘ (−∞,−1>u<0,1>
f'(x)>0 x∊(−1,0)∪(1,+∞) f↗ <−1,0>∪<1,+∞)
jak wyznaczyć fmax i fmin 

