Potrzebna dziedzina, pochodna,ekstremum lokalne, monotonicznosc, punkty przegiec
Justyna: POMOCY

Proszę zbadać przebieg zmienności funkcji : f(x)= x +
√1−x
27 mar 11:49
Jerzy:
Co potrafisz sama ?
27 mar 11:50
Justyna: Obliczyłam jak narazie dziedzinę, pochodna, ekstremum lokalne, aczkolwiek nie jestem pewna czy
dobrze i stroję w miejscu
27 mar 11:52
Jerzy:
Dawaj wyniki.
27 mar 11:52
Justyna: Dziedzina: x€ (−nieskończoność;1>
Pochodna: f'(x)= 1− 1/2√1−x
Miejsce zerowe: f(0)=1, f'(0)= 1/2
Ekstremum: x=3/4
27 mar 11:56
Jerzy:
Złe miejsce zerowe.
Po co Ci f'(0) ?
Jaki rodzaj ekstremum ?
27 mar 11:59
Justyna: Okej, pomyłka. Ekstremum lokalne
27 mar 12:04
Jerzy:
Maksimum, czy minimum ?
27 mar 12:05
Justyna: Minimum
27 mar 12:11
Jerzy:
Akurat maksimum.
Jeszcze granica w: − ∞.
27 mar 12:13
Justyna: Sory jednak maksimum
27 mar 12:14
Justyna: Funkcja jest rosnącą w przedziale (−
∞,3/4)
W 3/4 jest maksimum lokalne f (3/4)= 5/4
Funkcja jest malejąca w przedziale (3/4,1>
Ale nie wiem co się dzieję w 1. Należy ona do dziedziny funkcji.
Czy tak jest dobrze?
f'(1)=1−1/2
√1−1
f'(1)=1 ? Czy tak można to policzyć? Czy trzeba postawić 1 do funckji a nie pochodnej?
Nie wiem jak dalej obliczyć

27 mar 12:56
Jerzy:
Nic się nie dzieje ... f(1) = 1 + √1 − 1 = 1 + 0 = 0
27 mar 12:58
Jerzy:
Upss.... f(1) = 1
27 mar 12:58
Justyna: No to wtedy to 1 to jest wtedy maksimum czy minimum lokalne czy co?
27 mar 13:06
Jerzy:
Minimum lokalne.
27 mar 13:09
Leonard Euler: 1+0=0? hahaha
27 mar 16:38
Justyna : A jak późnej się oblicza punkt przegięcia? Wiem, że z drugiej pochodnej ale mam problem aby to
zrobic.
Myślę, ze druga pochodna wynosi: f''(x)=1/4√1−x
Dziedzina pochodnej to chyba Df': x∊(−∞,1)
A późnej chyba trzeba przyrównać dp zera ale cos mi nie wchodzi.
Mozesz mi polazac jak to rozwiazałeś?
27 mar 19:19
Janek191:
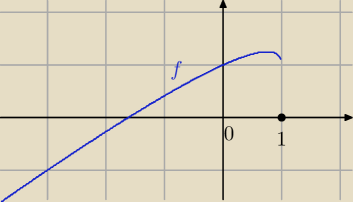
27 mar 19:22
Justyna: A jakieś obilczenia tego punktu?

27 mar 19:40
 Proszę zbadać przebieg zmienności funkcji : f(x)= x + √1−x
Proszę zbadać przebieg zmienności funkcji : f(x)= x + √1−x


