geometria trójkąt równoboczny szkoła średnia Niewiem: Z punktu P należącego do boku AB trójkąta równobocznego ABC poprowadzono półprostą dzielącą trójkąt na dwie figury o równych polach. Oblicz tangens kąta, jaki tworzy półprosta z odcinkiem AP, jeśli | AP | : | PB |=3

	4√3
W odpowiedziach jest :
	5

i zastanawiam się właśnie czy nie ma tam czasem błędu, ponieważ mi wyszło 2√29 zrobiłem to tak: D=punkt przecięcia boku AC jako że jest to trójkąt równoboczny to kąty są równe 60

	3		1
Przyjąłem że bok AB=a AP=		a PB=		a
	4		4

	√13
PD wyszło mi		a
	4

	1
odcinek od przecięcia wysokości w trójkącie APD z ramieniem AB do P		a
	12

nastepnie z własności trójkąta prostego obliczyłem cos szukanego kąta który wyszedł mi

	√13
	39

	2√29
z tego policzyłem sinus
	3√13

no i tangens wyszedł 2√29 Popełniłem gdzieś błąd czy jest on w odpowiedziach?

Jerzy: Problem w tym, że źle rozwiązujesz to zadanie. Długośc PD jest niepotrzebna do niczego.

Niewiem: A do obliczenia cos α z własności trójkąta protokątnego?

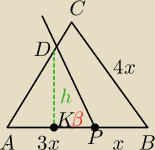
Jerzy: 1) Oblicz wysokość h

	1		1	(4x)2√3
		*3x*h =
	2		2	4

2) Oblicz długość odcinka AK:

	h
		= tg60o
	AK

3) Oblicz KP : KP = 3x − AK 4) Oblicz szukany tgβ:

	h
tgβ =
	KP

Jerzy:

	4x√3
1) h =
	3

	4
2) AK =		x
	3

	5
3) KP =		x
	3

	4x√3		3		4√3
4) tgβ =		*		=
	3		5x		5

Niewiem:

	1		1		(4x)2*√3
dziękuję, a dlaczego w 1)		*3x*h=		*
	2		2		4

Znaczy lewą stronę rozumiem ale dlaczego tak z prawej?

Niewiem: Oj,już zrozumiałem sam

Niewiem: Dziękuję bardzo, za odpowiedź, bardzo mi to rozjaśniło sytuację