geometria trójkąt dwusieczna szkoła średnia Niewiem: w trojkacie abc dlugosci bokow ac i bc sa odpowiednio rowne 2 i 4 zas miara kata acb wynosi 120 oblicz dlugosc odcinka ktory jest czescia wspolna dwusiecznej kata acb i trojkata abc robilem tak: trzeci bok AB = c dwusieczna = x dwusieczna przecina AB w punkcie D z tw kosinusa wyszedl c √28, potem licze AD z tw dwusiecznej 1/2=AD/DB, więc AD=y; DB=2y; więc

	√28
AD =
	3

z tw kosinusa licze CD powstaje row, kwadratowe i wychodza 2 wyniki 2/3 i 4/3 a w odpowiedzi jest tylko 4/3 prosze o jakies info dlaczego odrzucamy wynik 2/3. Było już pytanie o to na forum, ale nikt nie odpowiedział jak możemy wywnioskować że 4/3 jest właściwą odpowiedzią. Proszę o pomoc.

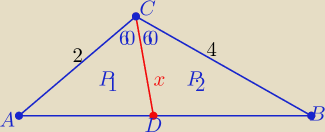
Eta: P(ABC)=P₁+P₂

1		1		1
	*2*4*sin120o =		*2*x*sin60o+		*x*4*sin60o
2		2		2

.......................... wyznacz x :

	4
x=
	3

Niewiem: Dziękuję za odpowiedź, widzę że udało się to w dużo prostszy sposób rozwiązać, ale dalej nie daje mi to odpowiedzi jak mogę zdefiniować, która odpowiedź jest prawdziwa jeśli zrobię moim sposobem.