zadanie optymalizacyjne Krakus:

	6x2−72x+210
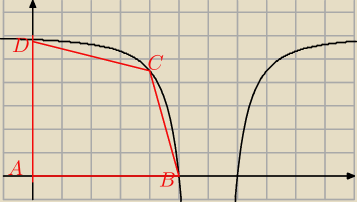
Na rysunku poniżej przedstawiono fragment wykresu funkcji
	x2−12x+36

określonej dla x ∈ (− ∞ ,6) . Wykres ten przecina osie Ox i Oy odpowiednio w punktach B i D , a punkt A jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty ABCD , w których punkt C leży na wykresie funkcji y = f(x) pomiędzy punktami B i D . Oblicz pierwszą współrzędną wierzchołka C tego z rozpatrywanych czworokątów, którego pole jest największe.

Krakus: Czy jest ktoś wstanie mi pomóc bo nie wiem jak zacząć?

===: 1) Napisz równanie prostej przechodzącej przez punkty B i D 2) Zauważ, że pole czworokąta ABCD będzie największe, gdy odległość punktu C od tej prostej będzie największa Powodzenia

Krakus: Dzięki

Janek191:

	6*( x2 − 12 + 35)		6*( x − 5)*( x − 7)
f(x) =		=
	x2 −12 x + 36		(x − 6)2

Mamy

	105		15		5
f(0) =		= 5		= 5
	18		18		6

	5
D = ( 0, 5		)
	6

B = ( 5, 0) więc

	6*( x − 5)*( x −7)
C = ( x,		}
	( x −6)2

piotr: pole:

	1
P(x) =		( f(0) x + 5 f(x))
	2

	32/3
P'(x) = 0 ⇒ x = 2 (3 −		)
	71/3