Styczna do okręgu kokoriko: Witam! Jak wyznaczyć drugą styczną w zadaniu: Napisz równania ogólne stycznych do danego okręgu o i przechodzących przez punkt A, jeśli o:x² + y² + 10x − 6y + 30 = 0, A(−7,9). Równanie ogólne okręgu: (x+5)² + (y−3)² = 4 środek okręgu to S(−5,3), r=2. Równanie ogólne prostej stycznej do okręgu i przechodzącej przez punkt A to ax−y+7a+9=0.

	|−5a−3+7a+9|
odległość środka okręgu od stycznej d=		= 2
	√a2+1

|2a+6|=2√a²+1 /² 4a²+24+36=4a²+4 24a=−32

	1
a=−1
	3

	1
b=−
	3

	4		1
y=−		x−
	3		3

y=4x+3y+1=0 A druga styczna to x+7=0 jak ja wyznaczyć?

===: ... i dlatego rysunek jest zawsze pomocny Chcesz wyznaczyć a ... czyli tgα ... tyle, że tg90^o to "mrzonka"

kokoriko: No właśnie z rysunku to łatwo odczytać. A jak mogę to inaczej policzyć?

piotr: możesz obliczyć punkt styczności z drugą prostą np przez napisanie równania okręgu o środku A i przechodzący przez punkt styczności pierwszej stycznej

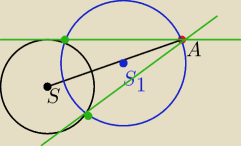
Powracający: Inny sposob (troche dlugi wynika z konstrukcji stycznej do okregu przechodzacej przez dany punkt z geometrii elementarnej 1. Liczymy dlugosc odcinka SA 2. polowa dlugosci odcinka SA to promien okregu ktory wyznaczy punkty stycznosci z danym okregiem w zadaniu 3. Wspolrzedne srodka odcika SA to srodek tego okregu 4. Przyrownujemny rownia okregow do siebie i mamy punkty stycznosci 5. Piszemy rownania prostych przechodzacych przez 2 punkty (rownania stycznych .

piotr: (x+5)² + (y−3)² = 4; (x+7)²+(y−9)²=(−7+17/5)²+(9−21/5)² ⇒x = −7, y = 3 x = −17/5, y = 21/5

kokoriko: Bardzo wam dziękuję