nierówności wielomianowe Nina : Wyznacz dziedzinę funkcji f jesli:

	4x3 +2
a) f (×)=
	√4 − 3x2 − x3

===: x³+3x²−4<0

Nina : A można nie podzielić przez −1 i wyjdzie dobra odpowiedź ?

===: MUSI

Nina : Wychodzi mi potem że x= −1 i x₁ , ×₂ = −2 Czyli wynik x € ( 1, +∞) A wynik powinien wyjść x € (−∞, −2) ∪ × € (−2, 1)

Nina : X € ( −1, +∞)

===: zauważ, że miejsca zerowe nie wchodzą

Nina : Jak to nie ?

===: bo < to nie to samo co ≤ a > to nie to samo co ≥

Nina: No tak. Ale jeśli nie ma miejsc zerowych to wynik Wychodzi ?

Powracający: Tu chodzi o to ze miejsca zerowe nie wchodza do zbioru rozwiazan tej nierownosci Masz nierownosc ostra czyli < (inaczej mniejsze od Natomiast nierownosc slaba ≤(inaczej mniejszse badz rowne cos tam

Nina: No dobrze ale to nie zmienia faktu ze wychodzi mi inny wynik niz powinien xd

Powracający: no bo pewnie ktorys jest pierwiastkiem podwojnym bo (x+2)(x−1) = x² przy najwyzszsej potedze , a masz miec x³ wychodza x=−2 i x=1 (ktorys jest podwojny

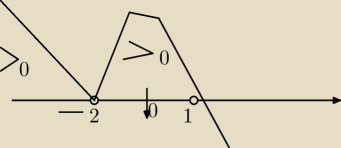
Powracający: Inaczej (x³+3x²−4 ) / (x−1)= x²+4x+4= (x+2)² czyli x=−2 jest pierwiastkiem podwojnym tam masz odbicie a nie przeciecie czyli −x³−3x²+4>0 dla x∊(−∞,−2)U(2,1)

Nina: Dziękuję <3