aaa
Maciek: zilustruj zbiór wszystkich punktów płaszczyzny których współrzedne (x,y) spełniają równanie
(x+5)(y−3)=0
proszę o pomoc, ponieważ w odpowiedziach jest inne rozwiązanie niż to które mi wychodzi
26 mar 15:03
Adamm: (x+5)(y−3)=0 ⇔ x+5=0 ∨ y−3=0
mamy 2 proste
x=−5 oraz y=3
26 mar 15:04
Maciek: czyli błąd w odpowiedziach

dzięki
26 mar 15:05
Maciek: a przykład:
a)|x|+|y|=3
b)|x|−|y|=1
?
26 mar 15:48
Jerzy:
Rozpatrujesz 4 przypadki w zależności znaku x i y
26 mar 15:49
Maciek: czyli
I) x>0 i y>0
II)x>0 i y<0
III) x<0 i y>0
IV)x<0 i y<0 ?
a b) nie można pokombinować z przeniesieniem |y| na prawą stronę?
26 mar 15:54
Adamm: raczej nie bardzo
26 mar 15:58
Maciek: Do którego pytania jest to odpowiedź?

26 mar 16:03
Adamm: do b)
26 mar 16:06
Maciek: dobra dzięki

jeszcze ostatni przykład
2|x|−|y+2|=1
26 mar 16:21
Maciek: czy to należy rozważyć w 3 przedziałach?
26 mar 16:37
Adamm: na 4 przedziałach
26 mar 16:37
Maciek: mógłbyś napisać jakie to przedziały?
26 mar 16:41
....e:
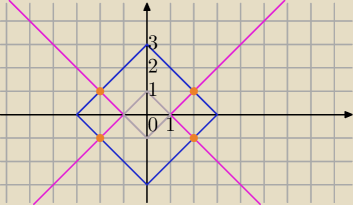
(1) |x|+|y|=3
|x|−|y|=1⇔|y|=|x|−1
do (1)
|x|+|x|−1=3
2|x|=4
|x|=2⇔x=2 lub x=−2
1) x=2 i |y|=2−1⇔|y|=1⇔y=1 lub y=−1
(2,1), (2,−1), (−2,1),(−2,−1)
26 mar 16:53
Maciek: A mógłbyś napisać przedziały również do:
2|x|−|y+2|=1 ?
26 mar 16:58
....e:
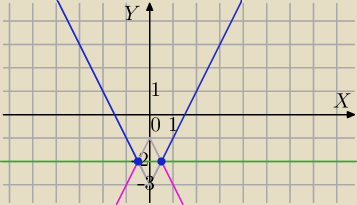
2|x|−|y+2|=1⇔
2|x|−1=|y+2|
1)
|y+2|=y+2 dla y≥−2 wtedy mamy:
y+2=2|x|−1
y=2|x|−3 i y≥−2 [ niebieski wykres]
2)
|y+2|=−y−2 dla y<−2
wtedy masz wzór:
−y−2=2|x|−1⇔−y=2|x|+1
y=−2|x|−1 punkty na wykresie tej funkcji leżące poniżej prostej y=−2
26 mar 19:00
 dzięki
dzięki

 jeszcze ostatni przykład
2|x|−|y+2|=1
jeszcze ostatni przykład
2|x|−|y+2|=1
 (1) |x|+|y|=3
|x|−|y|=1⇔|y|=|x|−1
do (1)
|x|+|x|−1=3
2|x|=4
|x|=2⇔x=2 lub x=−2
1) x=2 i |y|=2−1⇔|y|=1⇔y=1 lub y=−1
(2,1), (2,−1), (−2,1),(−2,−1)
(1) |x|+|y|=3
|x|−|y|=1⇔|y|=|x|−1
do (1)
|x|+|x|−1=3
2|x|=4
|x|=2⇔x=2 lub x=−2
1) x=2 i |y|=2−1⇔|y|=1⇔y=1 lub y=−1
(2,1), (2,−1), (−2,1),(−2,−1)
 2|x|−|y+2|=1⇔
2|x|−1=|y+2|
1)
|y+2|=y+2 dla y≥−2 wtedy mamy:
y+2=2|x|−1
y=2|x|−3 i y≥−2 [ niebieski wykres]
2)
|y+2|=−y−2 dla y<−2
wtedy masz wzór:
−y−2=2|x|−1⇔−y=2|x|+1
y=−2|x|−1 punkty na wykresie tej funkcji leżące poniżej prostej y=−2
2|x|−|y+2|=1⇔
2|x|−1=|y+2|
1)
|y+2|=y+2 dla y≥−2 wtedy mamy:
y+2=2|x|−1
y=2|x|−3 i y≥−2 [ niebieski wykres]
2)
|y+2|=−y−2 dla y<−2
wtedy masz wzór:
−y−2=2|x|−1⇔−y=2|x|+1
y=−2|x|−1 punkty na wykresie tej funkcji leżące poniżej prostej y=−2