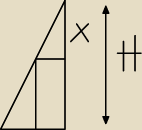 W metalowym ostrosłupie prawidłowym czworokątnym o wysokości H i krawędzi podstawy a wydrążono
otwór w kształcie walca, którego oś symetrii pokrywa się z osią symetrii ostrosłupa. Otwór
wydrążono przez podstawę ostrosłupa w ten sposób , że górna podstawa walca nie wystaje poza
powierzchnię ostrosłupa. Jaka może być najmniejsza możliwa objętość otrzymanej w ten sposób
bryły.
W metalowym ostrosłupie prawidłowym czworokątnym o wysokości H i krawędzi podstawy a wydrążono
otwór w kształcie walca, którego oś symetrii pokrywa się z osią symetrii ostrosłupa. Otwór
wydrążono przez podstawę ostrosłupa w ten sposób , że górna podstawa walca nie wystaje poza
powierzchnię ostrosłupa. Jaka może być najmniejsza możliwa objętość otrzymanej w ten sposób
bryły.
| r | ||||||||
= | |||||||||
| H | x |
| a√2x | ||
r= | ||
| 2H |
| a√2x | ||
V=π( | )2*(H−x) zał : xE(0,H) | |
| 2H |
| r | ||||||||
= | |||||||||
| H | x |
| ax | ||
r= | ||
| 2H |
| ax | ||
V=π( | )2*(H−x) | |
| 2H |
| a2x2 | a2Hx2−a2x3 | |||
V=π( | )(H−x)=π | |||
| 4H2 | 4H2 |
| (2a2Hx−3a2x2)(4H2)−0 | ||
V'(x)= | ||
| 16H4 |
| 8a2H3x−12a2H2x2 | ||
V'(x)= | ||
| 16H4 |
| 2H | ||
x=0 v x= | ||
| 3 |
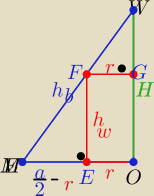 Z podobieństwa trójkątów MOW i FGW z cechy (kkk)
Z podobieństwa trójkątów MOW i FGW z cechy (kkk)
| MO | ME | H | |||
= | ⇒ hw=...= | (a−2r) , r∊(0,a/2) | |||
| OW | EF | a |
| 2 | ||
to Vw(r)= .... = Hπ(r2− | r3) | |
| a |
| 1 | ||
Odp: dla rmax= | a | |
| 3 |
| a2H(9−π) | ||
Vmax= | ||
| 27 |

| a2H(9−π) | ||
Odp: ma być Vmin= | ||
| 27 |