Funkcja sklejana Powracający: Dana jest funkcja okreslona wzorem f(x)= {−x²−3x dla x<−1 {2x²−x−1 dla x≥−1 Oblicz miejsca zerowe funkcji f Wyznacz najwieksza i najmniesza wartosc funkcji f w przedziale <−2,2> Wyznacz zbior wartosci parametru m dla ktorych rownanie |mx|= f(x) ma conajmnie dwa rozwiazania mam w odpowiedzi 3 miejsca zerowe ale nie bardzo wiem dlaczego 3 a nie 2 bo licze tylko dla x≥−1

Jerzy: A dlaczego tylko dla x ≥ −1 ?

Powracający: Dzien dobry . Wlasnie tego za bardzo nie rozumiem ( bo mysle ze x=0 to przedzial drugi ) wiec jesli mozesz to wyjasnij mi to . dziekuje .

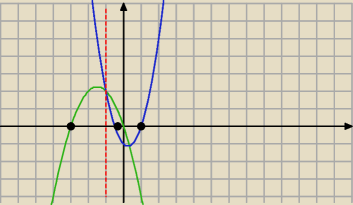
Jerzy: To te trzy miejsca zerowe.

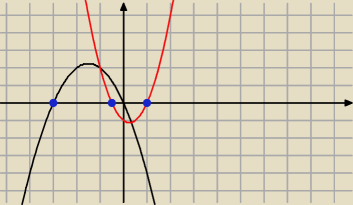
Powracający: Na wykresie widac ze beda 3 miejsca zerowe

Jerzy: Dla x < −1 "obowiązuje" wykres zielony, dla x ≥ 1 wykres niebieski.

Powracający: Jak to rozumowac algebraicznie ze tak powiem

Jerzy: Dla x ≥ −1 wymazujesz wykres czarny Dla x < −1 wymazujesz wykres czerwony

Powracający: Dobra łapie już to dzieki

Powracający: Jerzy Rozumuje to tak y=−x²−3x to x=−3 lub x=0 ale mam przedzial x∊(−∞,−1) wiec miejsce zerowe to x=−3 dla y= 2x²−x−1 to Δ= 9 x₁= 1 x₂= −0,5 (oba naleza do przedzialu <−1,∞) Teraz podpunkt c) Czy ma to zrobic graficznie ? czy trzeba jakies obliczenia . jesli tak to jakie . Zadanie na ocene celujaca

Powracający:

Jerzy: Zrób graficznie. Na celujący jest trochę liczenia. 1) Założenie: f(x) ≥ 0 2) mx = f(x) lub mx = −f(x) i analiza tych równań oddzielnie w obydwu przedziałach ( trójmiany kwadratowe z parametrem m)

Powracający: Dobrze sprobuje pozniej zrobic . Dzieki .

Powracający: pomoze ktos z tym sposobem algebraicznym to graficznie wychodzi mi m∊,−2,2> w podpunkcie c)

Powracający: jednak poprosilbym o pomoc .