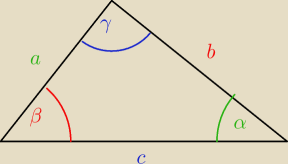
Geometria wykaż że Grześ: Wykaz, że jeżeli a, b, c są długościami boków trójkąta leżącymi na przeciwko odpowiednio kątów o miarach α≤β≤γ to a≤b≤c.

Powracający: Grzes masz udowodnic ze naprzeciwko mniejszsego boku lezy mniejszy kąt

Grześ: Widzę, że doszedłeś do tego samego co ja

Eta: Z tw. sinusów a=2Rsinα , b= 2Rsinβ, c=2Rsinγ i funkcja sinus na przedziale (0, π/2) jest rosnąca to a≤b≤c ⇒................

Grześ: Dziękuje

Eta:

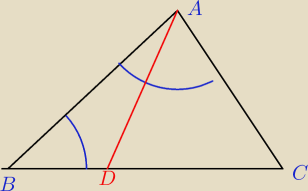
Powracający: twierdzenie W kazdym trojkacie naprzeci wiekszsego boku lezy wiekszy kat Zalozenie Bok BC >boku AC Teza kat BAC>kąta ABC Dowod jesli bok AC jest < od BC to na boku BC mozemy odlozyc odcinek CD rowny CA Polaczmy teraz punkt D z punktem A . Otrzymamy trojkat rownoramienny w ktorym kąty CDA i CAD sa rowne Ale kąt CDa jako kąt zewntrzny trojkata ABD jest wikszy od kąta ABC wobec czego i kąt CAD jest wiekszy od kąta ABC Poniewaz kąt CAD stanowi tylko czesc kąta BAC wiec kąt BAC jest wiekszy od kąta CAd a tym samym od kąta CDA A wiec jest tym bardziej wiekszy i od kąta ABC (poniewaz kąt ABC jest jeszce mniejszy od kąta CDA) cnd Tak samo dowiesc pozostalych bokow i kątow .