kwadratowa
Powracający: Zadanie maturalne
Dany jest wielomian
W(x)= x
2−mx+m
2−2m+1
a) dla jakiej wartosci parmetru m wielomian ten ma dwa rozne pierwiastki rzczywiste ktorych
suma jest o jeden wieksza od ich iloczynu
b) Niech m bedzie ta wartoscia parametru dla ktorej spelniony jest warunek opisany w punkcie
a)
Narysuj wykres funkcji g(x) = [W(x)] dla x∊<−2,2> wiedzac ze symbol [a] oznacza najwieksza
liczbe calkowita nie wieksza od a .
a) Δ>0
(−m)
2−4*(m
2−2m+1)>0
m
2−4m
2+8m−4>0
−3m
2+8m−4>0
Δ= 64−48=16
m
1= 2
(x
1+x
2)+1= x
1*x
2
m+1= m
2−2m+1
−m
2+3m=0
m
2−3m=0
m(m−3)=0 m=0 lub m=3
W odpowiedzi do tego podpunktu mam m=1
24 mar 23:43
Adamm: x1+x2=1+x1*x2
24 mar 23:50
Powracający:

m=m
2−2m+2
−m
2+3m−2=0
m
2−3m+2=0
Δ= 1
m
2= 2
b)
m=1 to W(x)= x
2−x+1−2+1
W(x)=x
2−x
g(x)= [x
2−x]
Ale to nie wiem jak
25 mar 00:09
Adamm: najpierw narysuj x2−x, potem sobie poradzisz
25 mar 00:11
Adamm:
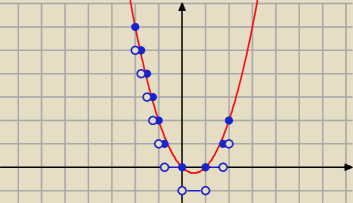
25 mar 00:14
Powracający:
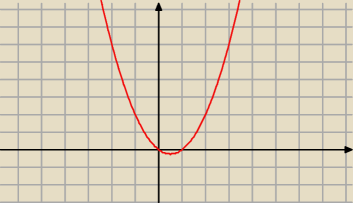
No niestety ale nie dam rady
25 mar 00:19
Powracający: Napisze odpowiedz
g(x)= 6 dla x=−2
| | 1 | |
=5 dla x∊ (−2, |
| (1−√21> |
| | 2 | |
| | 1 | | 1 | |
=4 dla x∊ ( |
| (1−√21, |
| (1−√17> |
| | 2 | | 2 | |
=3 dla x∊(0,5(1−
√17, 0,5(1−
√13>
=2 dla x∊(0,5(1−
√13, −1>U{2}
| | 1 | |
=1 dla x∊(−1, |
| (1−√5>U<0,5(1+√5),2) |
| | 2 | |
| | 1 | |
=0 dla x∊(0,5(1−√5),0>U<1, |
| (1+√5) |
| | 2 | |
= −1 dla x∊(0,1)
25 mar 00:42
Powracający: Poza tym dlaczego W(x)∊<−0,25 : 6> dla x∊<−2,2>
w(x)= x2−x to W(−2)= (−2)2−(−2)= 4+2=6 \W(2)= 22−2=2 przeciez
25 mar 00:49
Powracający: | | 1 | |
Juz wiem dlaczego W(x) ∊<− |
| ,6> dla x∊<−2,2> |
| | 4 | |
| | 1 | |
bo w tym przedziale q=− |
| |
| | 4 | |
Ale jak dojsc do tych obliczen ?
25 mar 01:00
Adamm: masz na myśli swój post 00:42

musisz sprawdzić dla jakich x odpowiednio
W(x)∊{0; 1; 2; 3; 4; 5; 6}
można ro zrobić rozwiązując 6 równań
ale nie wiem po co, możesz narysować to bez tej wiedzy,
i tak dla niektórych rozwiązania są niewymierne
25 mar 01:05
Powracający: Mozesz pokazac jedno z nich . Chcialbym to zrobic jak w tym poscie
25 mar 01:16
Powracający: Juz nie trzeba . Zrobilem . dzieki za pomoc
25 mar 01:48
 m=m2−2m+2
−m2+3m−2=0
m2−3m+2=0
Δ= 1
m=m2−2m+2
−m2+3m−2=0
m2−3m+2=0
Δ= 1

 No niestety ale nie dam rady
No niestety ale nie dam rady
 musisz sprawdzić dla jakich x odpowiednio
W(x)∊{0; 1; 2; 3; 4; 5; 6}
można ro zrobić rozwiązując 6 równań
ale nie wiem po co, możesz narysować to bez tej wiedzy,
i tak dla niektórych rozwiązania są niewymierne
musisz sprawdzić dla jakich x odpowiednio
W(x)∊{0; 1; 2; 3; 4; 5; 6}
można ro zrobić rozwiązując 6 równań
ale nie wiem po co, możesz narysować to bez tej wiedzy,
i tak dla niektórych rozwiązania są niewymierne