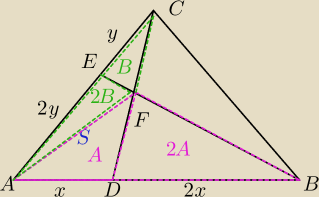
pola PrzyszlyMakler: W trójkącie ABC punkty D i E leżą odpowiednio na bokach AB i AC tak, że ADB = 1:2 oraz AE:EC =2:1. Wyznacz jaką częśc pola trójkąta ABC stanowi pole czworokąta ADFE. Pole szukane= S= P_ADFE Zauważyłem, że 2*P_ADF = P_DFB : oznaczmy to pole jako A 2*P_EFC=P_EFA: oznaczmy to pole jako B P_S= 2B + A Niestety nie wiem jak skończyć to zadanie, ani jak opisać pole trójkąta CFB Proszę o pomoc! Daję .

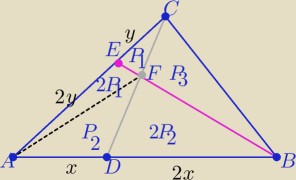Eta: W trójkątach ADC i DBC: 2(3P₁+P₂)=2P₂+P₃ ⇒ P₃=6P₁ W trójkątach ABE i BCE : 2P₁+3P₂=2(P₁+P₃) ⇒ 3P₂=2P₃ ⇒3P₂=12P₁ ⇒ P₂=4P₁ P(ADEF)=2P₁+P₂ = 6P₁ P(ABC)= 3P₁+3P₂+P₃= 3P₁+12P₁+6P₁=21P₁

	P(ADEF)
to		= ..........
	P(ABC)

Eta: Oddaj ....

aaa: To takie oczywiste gdy Ty to piszesz ech... Niemniej bardzo dziękuję !

aaa: Daje sad jabłek ! (Pisze z tel )

aaa: A gdyby tak się uprzec jak udowodnić że trójkąty ABE i ADC maja równe pola ?