Zadanie Majk: Dany jest trójkąt równaramienny ABC o bokach długości AB=10, AC=BC=10. Na boku AC zbudowano trójkąt ACD tak, że punkt D należy do prostej BA i DB=21. Punkt E należy do odcinka DC. Wykaż,

	2
że jeśli DE=7		. To AE||BC.
	7

Myślałem tu nad tw. odwrotnym do Talesa, ale nie potrafię znaleźć boku EC. Pomoże ktoś? Z góry dzięki.

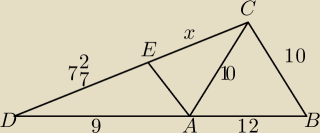
Majk: Chcę, znaleźć x, żeby chwycił Tales

===: Ty nawet treści zadania nie potrafisz przepisać

Jerzy: Trochę kultury .... 1) Oblicz wysokość ΔABC 2) Oblicz IDCI z tw. Pitagorasa.

Jerzy:

	68
x =		.... i tw. Talesa.
	7