Funkcja kwadratowa Powracający: Dane jest rownanie kwadratowe mx²−(m−2)x+m−3=0 a) Okresl wzor funkcji f(m)= x₁*x₂ gdzie x₁ i x₂ sa pierwiastkami danego rownania Ustal dziedzine i zbior wartosci tej funkcji a nastepnie sporzad jej wykres b) Podaj wszystkie wartosci parametru m dla ktorych dane rownanie ma dwa pierwiastki i oba sa wprzedziale (−∞,m) albo w przedziale (m,∞) Zadanie to chcialbym rozwiazywc etapami

	m−3
a) x1*x2=
	m

czyli teraz muszse policzyc delte i wyliczyc x₁ i x₂ Tak ? Prosze o odpowiedz na to pytanie jewsli bedzie tweirdzaca to zaraz policze

Jerzy: 1) m ≠ 0 2) Δ > 0

	m −3
3) f(m) =
	m

Powracający: Licze delte Δ=(−m+2)²−4*m(m−3)>0 Δ= m²−4m+4−4m²+12m>0 Δ= −3m²+8m+4>0 Δ= 64−48=16

	−8−4
m1=		=2
	−6

	−8+4		2
m2=		=
	−6		3

	2
m∊(		,2)
	3

Mozesz pokierowac dalej ?

Powracający: Zle Jeszcze raz licze Δ= −3m²+8m+4>0 Δ= 64−4*(−3)*4 Δ= 64+48= 112 112= 4*28= 4*4*7= 16*7 √112= 4√7

	−8−4√7		4+2√7
m1=		=
	−6		3

	4−2√7
m2= U{4−
	3

	4−2√7		4+2√7
m∊(		,		)
	3		3

Tak ma byc

Jerzy: Teraz ustal dziedzinę.

Powracający: Przepraszam ale musialem wyjechac . Nie za bardzo wiem jak

	m−3		3
ale f(m)=		= 1−		i m≠0
	m		m

I teraz mam do tego wzoru podstawic wyliczone m₁ i m−2 ?

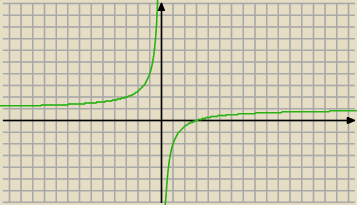
Jerzy: Tuataj masz wykres f(m) , teraz ogranicz go tylko do wyznaczonej dziedziny. Oblicz f(m₁) i f(m₂) i ustal zbiór wartości funkcji f(m)

Powracający:

	4−2√7		4+2√7
czyli dziedzina tej funkcji to <		,		>\{0}
	3		3

Wyszlo mi ze f(m₁)= 4+1,5√7 f(m₂)= 4−1,5√7 Zbior wartosci tej funkcji f(m)= <4−1,5√7, 4+1,5√7>

Powracający: Podpunkt b) zakladamy ze m≠0 i Δ≥0 dla przedzialu (−∞,m) x₁−m<0 x₂−m<0 to {(x₁−m)+(x₂−m)<0 {x₁−m)(x₂−m)>0 x₁+x₂<0 x₁*x₂−m(x₁+x₂)+m²>0 Dla przedzialu (m,∞) x₁−m>0 x₂−m>0 {x₁+x₂>0 x₁*x₂−m(x₁+x₂)+m²>0 I tutaj zastosuje wzory Vieta

Jerzy: W pierwszym ... źle policzone wartości funkcji w b) Dla (−∞,m) 1) Δ . 0 2) x_w < m 3) m*f(m) > 0 Dla: (m;+∞) 1) Δ > 0 2) x_w > m 3) m*f(m) > 0

Powracający: dziekuje (sprawdze a wydawalo mi sie ze mam dobrze .