nierówność Joko: Funkcja f określona jest wzorem f(x)=mx²+mx−1. Wyznacz te wartości parametru m, dla których funkcja f przyjmuje tylko wartości ujemne. Jako że m musi być malejące i funkcja nie może mieć miejsc zerowych to powstaje równanie m²+4m<0 I z tej nierówności podobno wynika, że m>−4 Czy to dlatego, ze kiedy dochodzimy do sytuacji m²<4m i dzielimy przez m to dzielimy przez liczbe ujemną, czyli znaki się zmieniają?

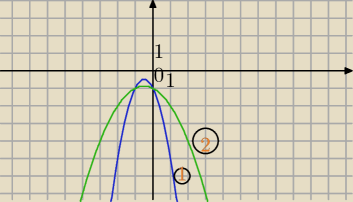
Mila: m<0 i Δ<0⇔ Δ=m²+4m<0 m*(m+4)<0 Parabola skierowana do góry [m∊(−4,0) ] i m<0⇔ m∊(−4,0) Przykłady 1) m=−2 f(x)=−2x²−2x−1

	1
m=−
	2

	1		1
2) f(x)=−		x2−		−1
	2		2

Joko: Jak zawsze czegoś nie zauważe... Nawet głupiej funkcji kwadratowej. Tak czy inaczej zastanawia mnie, vzy moje stwierdzenie jest prawidłowe dla tego jednego przypadku?

Mila: Poczytaj o funkcji kwadratowej. y=ax²+bx+c 1) a>0 , parabola skierowana ramionami do góry a>0 i Δ<0 parabola lezy nad osią OX ( przyjmuje tylko wartości dodatnie) 2) a<0 parabola skierowana ramionami w dół a<0 i Δ<0 parabola leży poniżej osi OX ( przyjmuje tylko wartości ujemne)

Joko: Ale ja jak najbardziej zdaje sobie sprawe z tych własności. Nie ważne, pomyliłem się.

Mila: Komentarz napisałam ponieważ masz tam bez sensu zapis− "m musi być malejące", stąd moje wątpliwości i wpis 20:06.