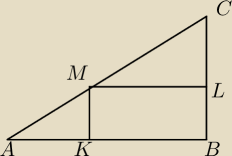
w trójkąt wpisano prostokąt umbro: W trójkąt prostokątny ABC o przeciwprostokątnej AC wpisano prostokąt KBLM (rysunek).

	|BL|		|BK|
Udowodnij, że		+		= 1
	|BC|		|BA|

Zauważyłem, że ΔABC ~ ΔAKM ~ ΔMLC (na podstawie cechy kąt−kąt−kąt), niestety nie wiem teraz, z których boków skorzystać, aby wykazać równość.

kochanus_niepospolitus: zauważ: |BK| = |LM|

	|LC|		|BC| − |BL|
ctg (∡BCA) =		=
	|LM|		|BK|

	|BC|
ale także: ctg (∡BCA) =
	|AB|

	|MK|		|BL|
a także: tg(∡CAB) =		=		= ctg (∡BCA)
	|AK|		|AB| − |BK|

|BC| − |BL|		|BL|		|BC|
	=		=
|BK|		|AB| − |BK|		|AB|

|BC| − |BL|		|BL|		|BC| − |BL|		|BK|
	=		⇔		=
|BK|		|AB| − |BK|		|BL|		|AB| − |BK|

(*)

	|BC|		|BK| − |AB| + |AB|
z (*)		− 1 =		⇔
	|BL|		|AB| − |BK|

	|BC|		|AB|		|BL|		|AB| − |BK|
⇔		=		⇔		=		⇔
	|BL|		|AB|−|BK|		|BC|		|AB|

	|BL|		|BK|		|BL|		|BK|
⇔		= 1 −		⇔		+		= 1
	|BC|		|AB|		|BC|		|BC|

c.n.w.