nie lada wyzwanie Pan X: Dany jest ostrosłup prawidłowy czworokątny o krawędzi podstawy wynoszącej a. Kąt między krawędzią boczną i podstawą jest równy kątowi płaskiemu przy wierzchołku ostrosłupa. Oblicz objętość ostrosłupa.

Jerzy: Przecież zadanie jest banalne. Zauważ,że przekrój pionowy przez przekątną podstawy jest trójkątem równobocznym. Oblicz: H i po zadaniu.

Pan X: nie nie nie

Pan X:

	a3
Odpowiedź brzmi V=		√1+√5
	6

Jerzy: Ile wynosi wysokość trójkąta równobocznego o krawędzi k*√2 ?

Pan X:

	√5−1
dostałęm jakieś wskazówki aby wyliczyć cosα który podobno bedzie równy
	2

Jerzy: miało być o krawędzi a.

Jerzy:

	√5 − 1
Zagalopowałem się ...ten trójkąt jest tylko równoramienny i faktycznie: cosα =
	2

krawędź boczna jest połową przekatnej podstawy i teraz policz H.

Pan X: jak udowodnic ze krawedz boczna jest polowa przekatnej podstawy

Jerzy: Nie, to nie jest prawdą ,źle zrozumiałem treść zadania, ale mając przekatną podstawy i cosα mozesz wyznaczyć wyskość bryły H , potem objetość.

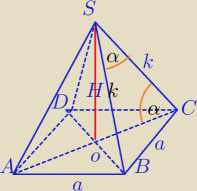
Mila: 1) ΔSOC:

	0.5a√2		0.5a√2
cosα=		⇔k=
	k		cosα

2) W ΔBCS: a²=k²+k²−2*k*k cosα a²=2k²*(1−cosα) , α− kąt ostry

	0.5a√2
a2=2*(		)2*(1−cosα)⇔
	cosα

1−cosα
	=1⇔
cos2α

cos²α+cosα−1=0 i cosα>0

	−1+√5
cosα=
	2

3)

	a√2
W SOC: k2=H2+(		)2
	2

	a2
z(2) k2=
	2*(1−cosα)

	a2		a2
H2=		−
	2*(1−cosα)		2

	a2		1		a2		1−1+cosα)
H2=		*(		−1)⇔H2=		*(
	2		1−cosα		2		1−cosα

	a2		cosα		a2		1
H2=		*		=		*
	2		1−cosα		2		1   −1 cosα

	a2		1
H2=		*		po wykonaniu działań
	2		2   −1 √5−1

	a2
H2=		*(√5+1)
	4

	a2		a
V=		*		*√√5+1
	3		2

	a3√1+√5
V=
	6

============

Eta: 2 sposób Korzystam z rys. Mili

	a√2
W ΔSOC cosα=		i w ΔBCS z twierdzenia kosinusów:
	2k

	2k2−a2		a2
cosα=		= 1−
	2k2		2k2

	a√2		a2
to		=1−		/*2k2
	2k		2k2

2k²−a√2k−a²=0 Δ_k=10a² , √Δ=√10a= √2*√5a i k>0

	a√2+√2*√5a		a√2		a2
k=		=		(√5+1) ⇒ k2=		(√5+3)
	4		4		4

Z tw. Pitagorasa w Δ SOC

	a√2		a2
H2=k2−(		)2 ⇒ H2=		(√5+1)
	2		4

	1		a3√√5+1
V=		*a2*H=.......=
	3		6