Oblicz cosinus, stereometria arew: Dany jest ostrosłup prawidłowy czworokątny. Stosunek długości krawędzi podstawy do krawędzi bocznej ostrosłupa jest równy 1:4. Wyznacz cosinus kąta między sąsiednimi ścianami bocznymi tego ostrosłupa. Proszę o pomoc..

arew: Nikt nic?

arew:

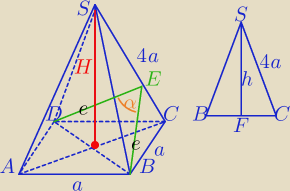
Mila: BE⊥SC i DE⊥SC W ΔDBE: (*) (a√2)²=e²+e²−2*e*e*cosα

	1		3√7
W ΔSFC: h2+		a2=16a2, h=
	4		2

	3a2√7
PΔBCS=
	4

	1
PΔBCS=		*4a*e
	2

	3a2√7
2a*e=
	4

	3a√7
e=		podstawiamy do (*)
	8

2a²=2e²*(1−cosα)

	2*9*7a2
2a2=		*(1−cosα)⇔
	64

	9*7
2=		*(1−cosα)
	32

	64
1−cosα=
	63

	64
1−		=cosα
	63

	1
cosα=−
	63