Zadanie na dowodzenie z planimetrii Paweł: zad. Przez punkt S leżący wewnątrz trójkąta ABC o polu P poprowadzono trzy proste równoległe do boków trójkąta. Te proste podzieliły trójkąt na sześć części , z których trzy są trójkątami o polach P₁, P₂, P₃.Wykaż,że √P=√P₁+√P₂+√P₃

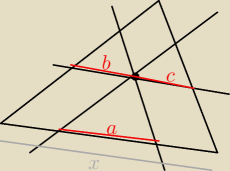
g: x = a+b+c wszystkie trójkąty są podobne, wiec ich pola są proporcjonalne do kwadratu podstawy. P = k*x², P₁ = k*a², P₂ = k*b², P₃ = k*c² √P/k = √P₁/k + √P₂/k + √P₃/k itd.

Paweł: Wiem, że trójkąty są podobne. Znam, twierdzenie o polach figur podobnych. Czy k oznacza skalę podobieństwa? A co z równoległobokami ?

Adamm: k to nie jest skala podobieństwa równoległoboki nie są częścią zadania