.. Ohma: Wyznacz wszystkie wartosci m dla ktorych rownanie (m−3)x²+mx+m+3 ma dwa rozne rozwiania nalezace do przedzialu (−∞;1)

kochanus_niepospolitus: warunki) 1) a≠0 2) Δ>0 3) x₁ < x₂ < 1

Ohma: A skad policzyc pierwiastki? Bo delta wychodzi −3m²+36

Ohma: Można przyjąć że x1+x2<2?

Alky: Najpierw liczysz Δ, a potem Δ_m , z tym że delta wyjdzie m²−12m+36

Alky: aj przepraszam, nie widziałem tego m, zwracam honor

Alky: 29:27 − tak

Alky: 19:27 *

kochanus_niepospolitus: nie można przyjąć x₁ + x₂ < 2 ... bo niech x₁ = −100, x₂ = 2 ... x₁ + x₂ < 2, a przecież oba te rozwiązania nie należą do zadanego przedziału

Alky: Ah, rzeczywiście. Głupotę palnąłem. Przepraszam za wprowadzenie w błąd. Może ja sam pójdę się coś pouczyć

Ohma: Więc co trzeba zrobić z tymi pierwiastkami jeżeli x+x się nie da?

Tomaszek: może a≠0 Δ>0 x_w<1 f(1)>0

kochanus_niepospolitus: Tomaszek ... f(x) = x² − 100 także będzie miał x_w < 1 (bo x_w = 0) ... ale x₂ = 10

kochanus_niepospolitus: oki ... nie zauważyłem f(1) > 0

kochanus_niepospolitus: to dobry tor, ale trza to 'dopieścić' : 1) a>0 Δ>0 x_w < 1 f(1) > 0 2) a<0 Δ>0 x₁<1 f(1)[C{<]]0 Bo przy tym co Tomasz napisał niestety (potencjalnie) połowę wyników odrzucamy

kochanus_niepospolitus: Tomaszek ... to co napisałeś niestety niosło za sobą taki oto błąd: niech f(x) = −x² + 100 ... x_w = 0 (ok) ... f(1) > 0 (ok) ... x₂ = 10 (nie jest ok )

Tomaszek: no tak już widzę

kochanus_niepospolitus: tam w 19:56 miało być nie: x₁ < 1 tylko x_w < 1

Ohma: O matko teraz to już nic z tego nie wiem

kochanus_niepospolitus: no to na spokojnie: rozpatrujemy dwa przypadki: 1) a> 0 (czyli ramiona 'do góry' ) Δ> 0 (co by były dwa pierwiastki) x_w < 1 (to pokazuje nam, gdzie jest wierzchołek −−− który przyjmować będzie ujemną wartość) f(1) > 0 (to w połączeniu z wiedzą, że wierzchołek jest 'na lewo od x=1' daje nam informację, że oba pierwiastki są 'na lewo' od x=1) drugi przypadek analogicznie, ale z ramionami 'na dół'

Jerzy: m − 3 ≠ 0 Trzy warunki: 1) Δ > 0 2) x_w < 1 3) a*f(1) < 0

Jerzy: Poprawka: 3) a*f(1) > 0

kochanus_niepospolitus: Jerzy ... a*f(1) > 0 ale poza tym to 'pozamiatałeś'

Jerzy: Tak się zdarza, jak się pisze telefonem

kochanus_niepospolitus: to nie pisz telefonem po klawiaturze ... użyj do tego palców

Ohma: Dlaczego a*f(1)?

kochanus_niepospolitus: bo jest to połączenie dwóch warunków jeżeli a>0 (ramiona do góry) to f(1) > 0 (bo przy x_w<1 wtedy mamy pewność pierwiastków w zadanym przedziale) analogicznie przy a<0 to f(1)<0 (taki sam argument) najlepiej sobie to narysuj

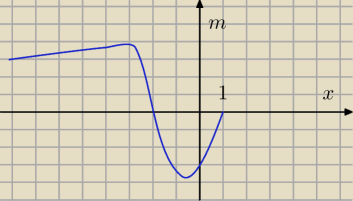
adam: Ciekawym sposobem na rozwiązanie jest przekształcenie równania (m−3)x²+mx+m+3=0 do postaci funkcji : m=(3 x² − 3)/(x² + x + 1) Rysujemy wykres tej funkcji z uwzględnieniem warunku z zadania x<1 i od razu widać, dla jakich m istnieją dwa rozwiązania, czyli co trzeba zrobić. W tym przypadku trzeba policzyć min, max oraz granicę x→−∞ tej funkcji. Rozwiązaniem są dwa przedziały: (m_min, x=1) oraz (lim x→−∞, m_max) czyli m∊(−2√3, 0)∪(3, 2√3)